CF 36E Two Paths

传送门

真实的自闭= =+

考试的时候老师明明说了可以路径为空T^T

然后光荣的挂掉了 20分的链【明明是最送分的】

上来就看出来欧拉回路了嘛 然后思考了一下大概奇点配个对 删一条简单路径剩下的跑欧拉路径就好了嘛 然后就冒出来了这个东西

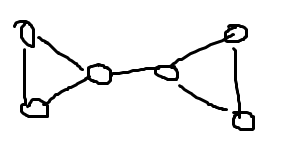
如果简单路径删了的话 图就不连通了= =||

心态崩塌【后来发现数据没卡这玩意T^T】

想新加边 但是发现这样就变成三段路径了= =||

然后孙神一眼切表示你强制第一步走新加的边就好了嘛

我好菜啊QAQ

于是就剩下一堆【真实的一堆】奇奇怪怪的细节

于是今天上午机房里弥漫着愉悦的hack气氛

具体处理什么的看代码吧QwQ

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<stack>
#define inf 20021225
#define ll long long
#define mxn 100010
using namespace std;

struct edge{int to,lt;}e[mxn<<1];
int d[mxn],cnt=1,in[mxn],n,m;
void add(int x,int y)
{
	e[++cnt].to=y;e[cnt].lt=in[x];in[x]=cnt;
	e[++cnt].to=x;e[cnt].lt=in[y];in[y]=cnt;
}
stack<int> st;bool vis[mxn],ag[mxn];
void eulerpath(int x)
{
	ag[x]=1;
	for(int &t=in[x];t;t=e[t].lt)
	{
		if(vis[t>>1])	continue;
		vis[t>>1]=1;int id=t>>1;
		eulerpath(e[t].to);
		st.push(id);
	}
}
int inq[mxn],sz;
void dfs(int x,int col)
{
	inq[x]=col;sz++;
	for(int i=in[x];i;i=e[i].lt)
	{
		if(inq[e[i].to])	continue;
		dfs(e[i].to,col);
	}
}
int q[6],tot;
int ans[mxn];
bool solve()
{
	if(m<2)	return false;
	int ltk=0,start[3];int i,nxt=0;
	for(int i=1;i<=n;i++)
	{
		if(!inq[i])
		{
			sz=0;dfs(i,ltk+1);
			if(sz>1)	start[++ltk]=i;
		}
	}
	if(ltk>2)	return false;
	for(int i=1;i<=n;i++)
	{
		if(d[i]&1)	q[++tot]=i;
		if(tot>4)	break;
	}
	if(tot>4)	return false;
	if(tot==2)	add(q[1],q[2]);
	if(tot==4)
	{
		if(ltk==2&&inq[q[1]]==inq[q[2]]&&inq[q[2]]==inq[q[3]])	return false;
		for(i=2;i<5;i++)	if(inq[q[i]]==inq[q[1]])	break;
		add(q[i],q[1]);
		if(i==2)	nxt=3,add(q[3],q[4]);
		if(i==3)	nxt=4,add(q[2],q[4]);
		if(i==4)	nxt=2,add(q[2],q[3]);
	}
	eulerpath(tot?q[1]:start[1]);
	int dis=0;
	if(!st.empty()&&st.top()>m)	st.pop();
	while(!st.empty())
	{
		int x=st.top();st.pop();
		if(x>m)	break;
		ans[++dis]=x;
	}
	if(dis==m)
	{
		//printf("QAQ");
		printf("%d\n",dis-1);
		for(int i=1;i<dis;i++)	printf("%d ",ans[i]);
		printf("\n");
		printf("%d\n%d\n",1,ans[dis]);
		return true;
	}
	printf("%d\n",dis);
	for(int i=1;i<=dis;i++)	printf("%d ",ans[i]);
	printf("\n");
	int tou=0;
	if(tot==4){if(!ag[q[nxt]])eulerpath(q[nxt]),tou=1;}
	else if(ltk==2){if(!ag[start[2]])eulerpath(start[2]);if(!ag[start[1]])eulerpath(start[1]);}
	dis=0;
	if(tou)	if(st.top()>m)	st.pop();
	while(!st.empty())
	{
		int x=st.top();st.pop();
		if(x>m)	break;
		ans[++dis]=x;
	}
	printf("%d\n",dis);//printf("QAQ");
	for(int i=1;i<=dis;i++)	printf("%d ",ans[i]);
	return true;
}
int main()
{
	int x,y;
	freopen("input.txt","r",stdin);
	freopen("output.txt","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)	scanf("%d%d",&x,&y),add(x,y),d[x]++,d[y]++;
	if(!solve())	printf("-1\n");
	return 0;
}

这一份是考试的改的 那个读入什么的有一些偏差qwq