浅谈Meet in the middle——MITM

目测观看人数 \(0+0+0=0\)

---

\(\mathrm{Meet\;in\;the\;middle}\)（简称 \(\rm MITM\)），顾名思义就是在中间相遇。

可以理解为就是起点跑搜索树基本一半的状态，终点也跑搜索树基本一半的状态，最后撞到中间，一种类似双向 DFS 的东西。优化还是不错的awa，减少了差不多一半。

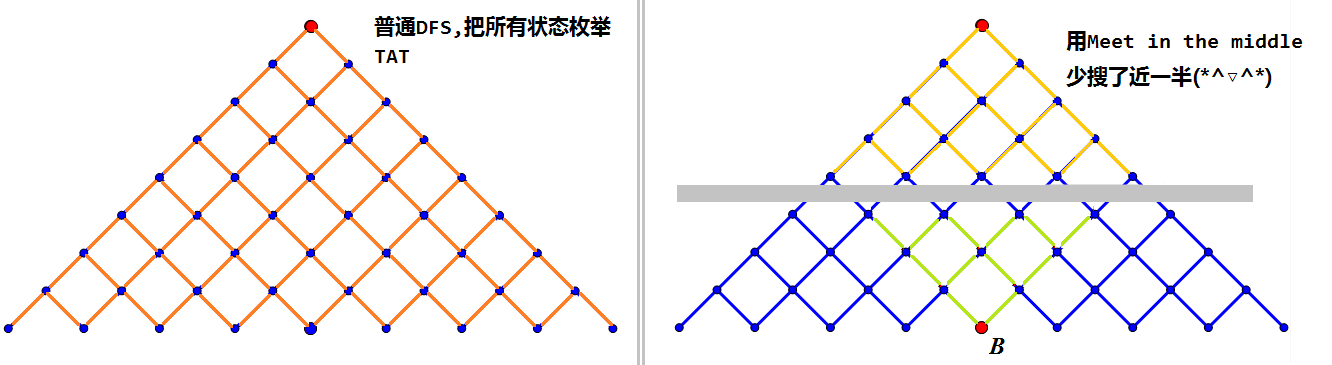
时间复杂度可如下分析：

设向外搜索 \(n\) 层需要的代价为 \(k(n)\)。如果不用 \(\textrm{MITM}\)，那么复杂度显然是 \(\mathcal O(k(n))\)。

以下提供两种做法：

• 方法 \(1\)：由 \(\rm MITM\) 定义得，从起点搜索到一半的代价为 \(k\left(\dfrac{n}{2}\right)\)，从终点搜索到一半的代价也为 \(k\left(\dfrac{n}{2}\right)\)，总代价为 \(2\cdot k\left(\dfrac{n}{2}\right)\)，省略常数，得时间复杂度 \(\mathcal O\left(k\left(\dfrac{n}{2}\right)\right)\)。
• 方法 \(2\)：设搜索树起点与终点为 \(A,B\) 连接 \(B\) 与搜索树左右边缘中点，再连接两个左右边缘中点，将搜索树分为四个面积相等区块，\(\rm MITM\) 仅搜索其中两个区块，得时间复杂度为 \(\mathcal O\left(k\left(\dfrac{n}{2}\right)\right)\)。

这种算法吧，对于 \(k(n)=n^2\) 时，朴素算法为 \(n^2\)，\(\rm MITM\) 为 \(\left(\dfrac{n}{2}\right)^2=\dfrac{n^2}{4}\)，优化了 \(\dfrac{1}{4}\) 复杂度。线性的优化，在数据大时效果明显。但是如果 \(k(n)=2^n\)，那么朴素算法为 \(2^n\)，\(\rm MITM\) 为 \(2^{\frac{n}{2}}=\sqrt{2^n}\)。

---

• 例题1

显然从一个节点出发进行搜索这题肯定会超时的

对于一个 \(9\) 位数，一共有 \(9\) 种可能的 \(+1\) 操作（每一个数位都可以 \(+1\)），一共有 \(8\) 种可能的交换操作，共 \(17\) 种操作。乘法原理得如果向外搜 \(10\) 层复杂度是 \(17^{10}\)使用某 Windows 常用计算小工具得 \(17^{10}=2015993900449\) 假设计算机 \(1ms\) 运行 \(10^4\) 次操作还是不能 \(1s\) 解决，显然 \(\bold{\rm TLE}\)。

告诉起始点来个 \(\rm MITM\) 双向就珂以了，\(17^5=1419857\)，就算是 \(1ms\) 跑 \(10^2\) 的老爷机跑的差不多才 \(0.1s\)。

这题 \(\rm BFS\) 可能会浪费点时间还是 \(\rm DFS\) 好awa

注意用个 \(\rm hash\)，别 \(\rm MLE\) 了

• 例题2

原题在 \(\rm codevs\) 众所周知 \(\rm codevs\) \(\dots\dots\)

有 \(n\) 个砝码，现在要称一个质量为 \(m\) 的物体，请问最少需要挑出几个砝码来称？

注意一个砝码最多只能挑一次。

\(1\le n\le 30\)，\(1\le m\le 2^{31}\)，\(1\le \text{每个砝码的质量}\le 2^{30}\)

看起来像是背包？？（

• 解法 \(1\)：暴！力！出！奇！迹！一发爆搜切！掉！！
  
  记得优化awa

  1. 用后缀和优化
  2. 用读优
  3. 如果当前使用的砝码数 \(\ge\) 当前最优解，\(\rm return\)（最优性剪枝）；
  4. 深搜之前按从大到小排序（改变搜索顺序），\(\text{当前总重量}+\text{当前砝码重量}<m\)（最优性剪枝） ，\(\rm return\)；
  5. 如果 \(\text{当前总重量}+\text{当前砝码重量}>m\) ，换下一个砝码（可行性剪枝），注意不要 \(\rm return\)；

  然后就可以写出代码了：
  
  

• 解法 \(2\)：用 \(\rm MITM\)，如果后 \(\dfrac{1}{2}\) 发现有 \(=m\) 的就更新答案，这个稳过，不用优化。
  
  代码：