hdu 5033 buiding（单调栈）

hdu 5033 buiding（单调栈）

某年某月某天，马特去了一个小镇。这个小镇如此狭窄，以至于他可以把小镇当作一个枢纽。在镇上有一些摩天大楼，其中一栋位于xi，高度为hi。所有的摩天大楼位于不同的地方。为了简化题目，假设摩天大楼没有宽度。由于摩天大楼如此之高，马特几乎看不到天空。对于马特所在的位置，他想知道他能看到天空的角度范围有多大。假设马特的身高是0。可以保证，对于每个查询，马特的左右两边至少有一座建筑物，而且他的位置上没有建筑物。建筑物的数量n<1e5，查询次数Q<1e5。

我用常规思路，想不出什么好方法。既然这道题的普遍解法是单调栈，那么我们就来看一下单调栈怎么实现。首先，单调队列和单调栈的前提是，加入的元素满足一种有序的关系。所以我们自然而然地就想到，将所有查询排序，从左向右和从右向左分别进行查询的计算。以从左向右为例，如何做到在（均摊）O1的时间内找到一个查询的答案呢？我们先来找些性质。

性质1：如果一个建筑物i比它左侧的j高，那么当i和j都在马特左侧时，马特一定看不到j。也就是说，如果维护一个关于建筑物下标的单调栈，新加进来一个建筑时，可以把它左侧所有更矮的建筑删掉。那么，现在的单调栈就是单调递减的。这就去除了第一种冗余状态。

性质2：从左向右而言，如果有这样的情况：

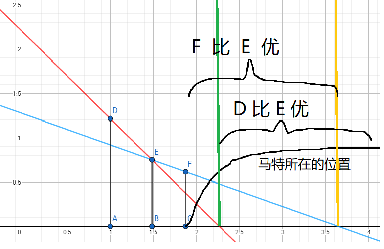
，也就是单调栈中的顶上两个建筑和新加进来的建筑组成一个凹包（不好意思，下凸包）,那么可以直接把单调栈顶的建筑删了，一直循环删下去。因为无论马特怎么站，都不会被它挡住。第二种冗余状态也被我们去除了。那么现在，单调栈存储的建筑就组成了一个上凸包。

性质3：然而，优化力度还不够大。这样子算法依然不是O(n)的。那怎么办呢？

由于马特一直往右跑，那么他与凸包相切的点只会往左移动：

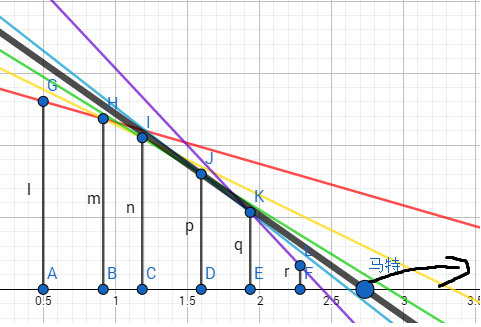
所以，在加入新的建筑之后，判断一下马特与当前凸包的交点，然后将交点右侧的建筑全删了（弹出）即可。栈顶的建筑就是最优建筑（切线嘛）。这就去除了第三种冗余状态。然而这样的时间复杂度是均摊O(1)的吗？额，显然的。

这可能是目前为止我写的最详细的一篇博文。。

#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;

const int maxn=1e5+5;
const double pi=3.1415926535898;
struct stack{
    int t, a[maxn];
    void push(int x){ a[++t]=x; }
    void pop(){ if (--t==-1) ++t; }
    void reset(){ t=0; }
    inline int top(){ return a[t]; }
    inline int top2(){ return a[t-1]; }
}s;
struct query{
    int id, ans1, ans2; double x;
}q[maxn], q2[maxn];
struct building{
    double x, h;
}b[maxn];

int n, T, Q;

bool cmp1(query &a, query &b){
    return a.x<b.x; }
bool cmp2(query &a, query &b){
    return a.id<b.id; }
bool cmpb(building &a, building &b){
    return a.x<b.x; }

double angle(double x, double y){
    return atan(x/y)*180/pi;
}

int main(){
    scanf("%d", &T); int tmp=0;
    while (T--){
        ++tmp; s.reset();
        scanf("%d", &n);
        for (int i=1; i<=n; ++i)
            scanf("%lf%lf", &b[i].x, &b[i].h);
        scanf("%d", &Q);
        for (int i=1; i<=Q; ++i){
            scanf("%lf", &q[i].x);
            q[i].id=i;
        }
        sort(b+1, b+n+1, cmpb);
        sort(q+1, q+Q+1, cmp1);
        int nowbui=1; s.push(1);
        for (int i=1; i<=Q; ++i){
            while (b[nowbui+1].x<q[i].x){ //从左到右加入建筑物
                ++nowbui;
                //第一种冗余状态：左边的楼比右边的矮
                while (s.t>0&&b[s.top()].h<=b[nowbui].h) s.pop();
                //所以现在这个建筑物序列严格下降
                //第二种冗余状态：是个下凸函数
                while (s.t>1&&(b[nowbui].h-b[s.top()].h)/
                       (b[nowbui].x-b[s.top()].x)>=
                       (b[s.top()].h-b[s.top2()].h)/
                       (b[s.top()].x-b[s.top2()].x)) s.pop();
                //所以现在这个建筑物序列是凸包了
                s.push(nowbui);
            }
            //第三种冗余状态：若一栋楼在视线所切的那栋楼的右边，则可以删去
            //可以用均摊，证明这里的复杂度是常数
            while (s.t>1&&(b[s.top2()].h)/(q[i].x-b[s.top2()].x)>
                   (b[s.top()].h)/(q[i].x-b[s.top()].x)) s.pop();
            //现在终于不仅排除了冗余状态，并且找到了最优解。
            q[i].ans1=s.top();
        } //从右往左也一样
        nowbui=n; s.reset(); s.push(n);
        for (int i=Q; i>=1; --i){
            while (b[nowbui-1].x>q[i].x){
                --nowbui;
                //右边的楼比左边的矮
                while (s.t>0&&b[s.top()].h<=b[nowbui].h) s.pop();
                //下面有图 (其实这里封装一个关于斜率的函数会更好)
                while (s.t>1&&(b[nowbui].h-b[s.top()].h)/
                       (b[nowbui].x-b[s.top()].x)<=
                       (b[s.top()].h-b[s.top2()].h)/
                       (b[s.top()].x-b[s.top2()].x)) s.pop();
                s.push(nowbui);
            }
            //下面有图
            while (s.t>1&&b[s.top2()].h/(b[s.top2()].x-q[i].x)>
                   b[s.top()].h/(b[s.top()].x-q[i].x)) s.pop();
            q[i].ans2=s.top();
        }
        sort(q+1, q+Q+1, cmp2);
        printf("Case #%d:\n", tmp);
        for (int i=1; i<=Q; ++i){
            printf("%.5lf\n", 180-angle(b[q[i].ans1].h,
                q[i].x-b[q[i].ans1].x)-angle(b[q[i].ans2].h,
                    b[q[i].ans2].x-q[i].x));
        }
    }
   // printf("%.6lf", angle(1, 1));
    return 0;
}