SPOJ：Bits. Exponents and Gcd（组合数+GCD）

Rastas's has been given a number n. Being weak at mathematics, she has to consider all the numbers from 1 to 2n - 1 so as to become perfect in calculations. (You can assume each number is consider as a soldier).

We define the strength of number i as the number of set bits (bits equal to 1) in binary representation of number i.

If the greatest common divisor of numbers a and b is gcd(a, b),

Rastas would like to calculate the function S which is equal to: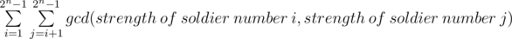 

As the friend of Rastas, it's your duty to calculate S modulo 109 + 7.

Input

The first line of the input contains the number of test cases, T. Each of the next T lines contains an integer n, as mentioned in the question

Output

For each value of n given, find the value of the function S.

Constraints

Sum of n over all test cases doesn't exceed 2500.

Example

Input:
3 

1 

2 

5

Output: 

0 

3

680

题意：给定N，求,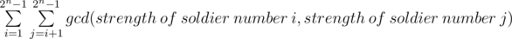

即对这些(i,j)，将i和j表示成二进制，累加i和j的二进制里1的个数的gcd。

思路：考虑靠2^N-1很大，直接针对二进制考虑，因为最多有2500个1，O(N^2)可以暴力搞定。我们考虑组合数，枚举有X个1的个数个Y个1的(i,j)，贡献是nun[X]*num[Y]*gcd(X,Y)。当X等于Y时，减去自己。其中num[X]=C(X,N);

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int Mod=1e9+;
int c[],fac[];
int qpow(int a,int x){
    a%=Mod; int res=;
    while(x){ if(x&) res=(ll)res*a%Mod; a=(ll)a*a%Mod; x>>=; } return res;
}
int main()
{
    int N,M,i,j,T,ans;
    fac[]=; for(i=;i<=;i++) fac[i]=(ll)fac[i-]*i%Mod;
    scanf("%d",&T);
    while(T--){
        ans=; scanf("%d",&N);
        for(i=;i<=N;i++){
            c[i]=(ll)fac[N]*qpow(fac[i],Mod-)%Mod*qpow(fac[N-i],Mod-)%Mod;
        }
        for(i=;i<=N;i++) {
            for(j=;j<=N;j++){
                if(i!=j) ans=(ans+(ll)c[i]*c[j]%Mod*__gcd(i,j))%Mod;
                else ans=(ans+(ll)c[i]*(c[i]-)%Mod*i)%Mod;
            }
        }
        ans=(ll)ans*qpow(,Mod-)%Mod;
        printf("%d\n",ans);
    }
    return ;
}