bzoj2693

线性筛+莫比乌斯反演

盗波图 来自candy?大神

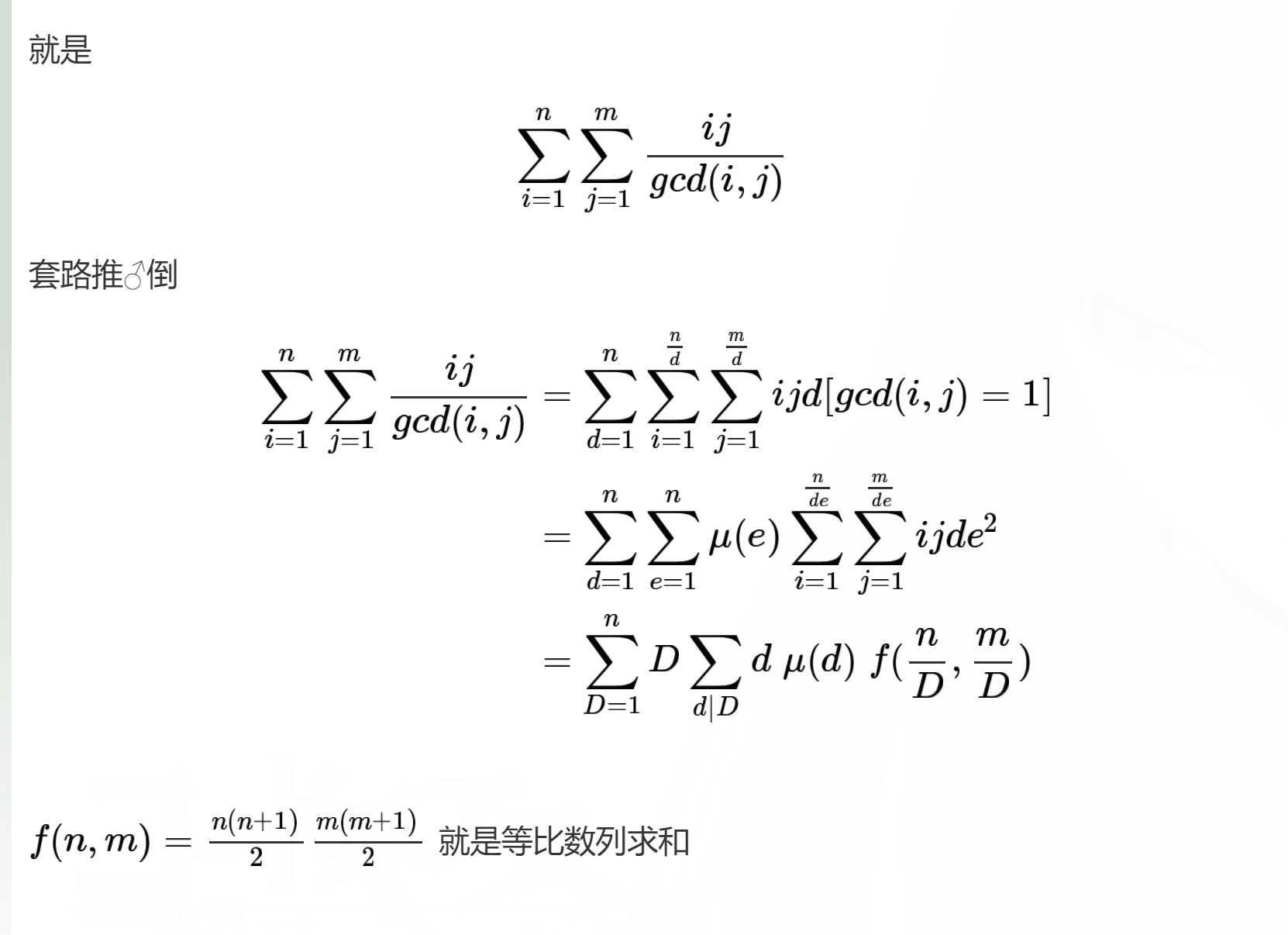
反演很重要的一条公式就是[gcd(i,j)==1]=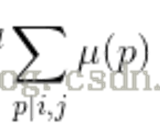

线性筛怎么推呢？

我们分4个步骤，1.先推出f[1]，2.推出f[p],p是一个质数，3.由于线性筛筛的是积性函数，那么当gcd(i,p[j])==1的时候，f[i*p[j]]=f[i]*f[p[j]],4.前三步都比较简单，第四步是if(i%p[j]==0)该怎么办

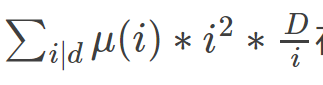
我们是要推这个东西的值，因为积性函数的约数和也是积性函数，所以这个也可以筛，那么我们考虑对于当前的D，我们用一个pri筛到了D,而且D%pri==0,然后思考一下，这个pri能给这个式子带来什么贡献呢?

很明显，i肯定是几个质数的乘积，否则mu[i]==0，没有意义，那么这个pri肯定对约数和没有贡献了，因为之前筛到的时候已经被计算过了，那个*i^2自然也是不可能受到pri的影响，但是我们看看那个D,现在我们求的是f[D*pri],那么自然D得乘上pri，所以我们得出现在f[i*pri]=f[i]*pri

大概是这样吧

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = , mod = ;
int n, m, T;
int mu[N], p[N];
bool mark[N];
ll f[N];
void ini()
{
    mu[] = f[] = ;
    for(int i = ; i <= ; ++i)
    {
        if(!mark[i])
        {
            p[++p[]] = i;
            mu[i] = -;
            f[i] = ((-(ll)i * (ll)i + i) % mod + mod) % mod;
        }
        for(int j = ; j <= p[] && i * p[j] <= ; ++j)
        {
            mark[i * p[j]] = ;
            if(i % p[j] == )
            {
                mu[i * p[j]] = ;
                f[i * p[j]] = f[i] * p[j] % mod;
                break;
            }
            f[i * p[j]] = f[i] * f[p[j]] % mod;
            mu[i * p[j]] = -mu[i];
        }
    }
    for(int i = ; i <= ; ++i) f[i] = (f[i] + f[i - ]) % mod;
}
ll Sum(ll x, ll y)
{
    return (x * (x + 1ll) / 2ll % mod) % mod * (y * (y + 1ll) / 2ll % mod) % mod;
}
void solve(int n, int m)
{
    if(n > m) swap(n, m);
    ll ret = ;
    for(int i = , j = ; i <= n; i = j + )
    {
        j = min(n / (n / i), m / (m / i));
        ret = (ret + Sum(n / i, m / i) % mod * ((f[j] - f[i - ]) % mod + mod) % mod) % mod;
    }
    printf("%lld\n", ret);
}
int main()
{
    ini();
    for(cin >> T; T; --T)
    {
        scanf("%d%d", &n, &m);
        solve(n, m);
    }
    return ;
}