SPFA

SPFA算法用来求单源最短路。可以处理任何有解的情况。

先建一个数组\(dist_x = 起点到x的最短路长度\)，当\(x=起点\)时为0，当x和起点不通时为INF（本题中为\(2^31-1\)）。

明确一下松弛的概念。考虑节点\(u\)以及它的邻居\(v\)，从起点跑到v有好多跑法，有的跑法经过\(u\)，有的不经过，那么经过\(u\)的跑法的距离就是\(dist_u + u到v的距离\)。所谓松弛操作，就是看一看\(dist_v\)和\(dist_u + u到v的距离\)哪个大一点，如果前者大一点，就说明当前的不是最短路，就要赋值为后者，这就叫做松弛。松弛，英文中是叫relax的，为什么叫这个名字我也不知道。

接着维护一个队列，保存待松弛的节点。一开始设起点的dist为0，然后把起点放进队列里。然后就开始循环，如果队空就说明全部节点都松完了，可以退出循环，没空就要继续松。把队列第一个元素拉出来，然后依次松弛它的邻居，对于每个邻居，如果松弛成功了，就看看那个邻居在不在队里，如果不在队里就把那个邻居扔进队尾。

下面\(\pi\)代表起点，\(\lambda\)表示某个节点，\(\delta\)表示邻居，\(\zeta_\lambda\)表示起点到\(\lambda\)的距离，\(\xi_{\lambda,\delta}\)表示\(\lambda到\delta的距离\)，\(\kappa_\lambda\)表示\(\lambda\)是否在队列中。

1. \(\zeta_{\{1\dots n\}} = \infty\)
2. \(\zeta_\pi = 0\)
3. 新建一个空队列\(\phi\)
4. 往\(\phi\)里加\(\pi\)，\(\kappa_\pi = 1\)
5. while \(\phi\)非空
6.   \(\lambda\) = pop \(\phi\)，\(\kappa_\lambda = 0\)
7.   for \(\delta \in \lambda的邻居\)
8.     if $ \zeta_\delta > \zeta_\lambda + \xi_{\lambda,\delta}$
9.       \(\zeta_\delta = \zeta_\lambda + \xi_{\lambda,\delta}\)
10.       if \(\lnot \kappa_\delta\)
11.         往\(\phi\)里加\(\delta\)，\(\kappa_\delta = 0\)

---

别人的文章

原文 20160517

差分约束系统

一般来说，对于一类“两个未知数的差小于等于（或大于等于）某个常数” (xi−xj≤c)(xi−xj≤c) 不等式组的求解，便是差分约束系统。差分约束系统的美妙之处在于可以将其转为图论，通过求解单源最短路来判断原不等式组是否有解甚至求得最大或最小解。

首先，显然对于此类不等式组，要么无解，要么有无数解。因为假设存在一组解为 x1,x2,…,xnx1,x2,…,xn，那么对于任意一个常数 kk，x1+k,x2+k,…,xn+kx1+k,x2+k,…,xn+k 也必是一组解，因为他们的差值是不变的，所以不等式组依然成立。

接下来考虑单源最短路图，对于某点 vv 与其邻接点 uu，显然 dist[v]≤dist[u]+costu−>vdist[v]≤dist[u]+costu−>v，也即 dist[v]−dist[u]≤costu−>vdist[v]−dist[u]≤costu−>v，正好满足“两个未知数的差小于等于某个常数”。因此，我们将待求解不等式组中的未知数看成图上的顶点，对于每个不等式 xi−xj≤cxi−xj≤c，转化成图中顶点 ii 向 jj 建边，边权为 cc。

然后直接在建成的图上跑单源最短路就可以了。如果存在负环则无解，否则 dist[i]dist[i] 便是其中一组解，至于以哪个点作为源点都是可以的。相当于以哪个点作为源点就是将该点赋值为 00，通过该约束去得出不等式组中其他未知数的解。

还有一种是不仅需要判断是否有解，还要求求出一组最大/最小解，这种类型可以考虑通过增加一个点去对其他点进行约束，然后以这个点为源点跑最长/最短路求解，由于差分约束类型题目近几年几乎不可见了，所以基本没遇过这种类型，只能瞎BB下。

SPFA 算法

由于图中可能存在负环，所以不能使用 dijkstradijkstra 算法求解，可以考虑使用 SPFASPFA 或者 Bellman−FordBellman−Ford，个人建议用 SPFASPFA ，比较快。

最长路与最短路

SPFASPFA 求最长路的算法跟求最短路类似：

最长路是初始化为 00，当存在 dist[v]<dist[u]+costu−>vdist[v]<dist[u]+costu−>v 时进行更新。

最短路时初始化为 INFINF，当存在 dist[v]>dist[u]+costu−>vdist[v]>dist[u]+costu−>v 时进行更新。

---

P3371 【模板】单源最短路径

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：

4 6 1

1 2 2

2 3 2

2 4 1

1 3 5

3 4 3

1 4 4

输出样例#1：

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

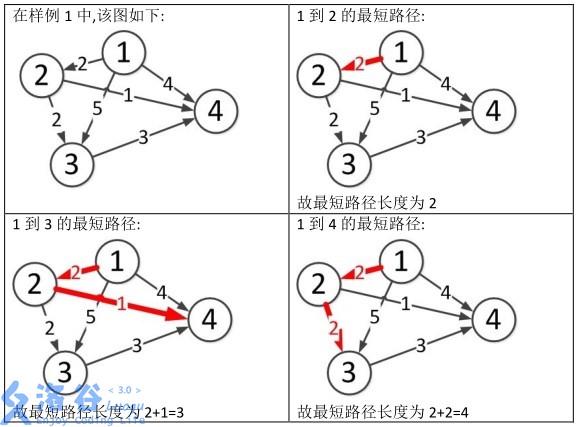
样例说明：

---

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>

    namespace nr3371 {

using std::fill;
using std::queue;
using std::vector;

        namespace io {

inline int read(void) {
    int x;
    scanf("%d", &x);
    return x;
}

        } // namespace io

using io::read;

const int errcode = 2147483647;

inline void read_graph(void);
inline void spfa(void);
inline void print_result(void);

inline void main(void) {
    read_graph();
    spfa();
    print_result();
}

//--------------------------------------------------

int point_cnt, edge_cnt, source;

const int point_cnt_max = 1e4 + 100;
const int edge_cnt_max  = 5e5 + 100;

struct edge_t {
    int dst;
    long weight;
};

vector<edge_t> edges[point_cnt_max];

inline void read_graph(void) {
    for (int i = 0; i < point_cnt; ++i) {
        edges[i].clear();
    }

	point_cnt = read();
	edge_cnt  = read();
	source    = read();

	for (int i = 0; i < edge_cnt; ++i) {
	    int src = read();
        edge_t e;
        e.dst = read();
        e.weight = read();

        edges[src].push_back(e);
    }
}

// --------------------------------------

long dist[point_cnt_max];

inline void spfa(void) {
    fill(dist, dist+point_cnt_max, errcode);
    dist[source] = 0;

    vector<bool> vis(point_cnt+1);
    fill(vis.begin(), vis.end(), false);
    vis[source] = true;

    queue<int> q;
    q.push(source);

    while (!q.empty()) {
        int x = q.front();
        q.pop();
        vis[x] = false;

        for (vector<edge_t>::iterator it = edges[x].begin(); it != edges[x].end(); ++it) {
            if (dist[it->dst] > dist[x] + it->weight) {
                dist[it->dst] = dist[x] + it->weight;

                if (!vis[it->dst]) {
                    vis[it->dst]  = true;
                    q.push(it->dst);
                }
            }
        }
    }
}

// --------------------------------------

inline void print_result(void) {
    for (int i = 1; i <= point_cnt; ++i) {
        printf("%ld ", dist[i]);
    }

    putchar('\n');
}

    } // namespace nr3371

int main(void) {
    //freopen("in.txt", "r", stdin);

    nr3371::main();
    return 0;
}

P2384 最短路

题目背景

狗哥做烂了最短路，突然机智的考了Bosh一道，没想到把Bosh考住了...你能帮Bosh解决吗？

他会给你100000000000000000000000000000000000%10金币w

题目描述

给定n个点的带权有向图，求从1到n的路径中边权之积最小的简单路径。

输入输出格式

输入格式：

第一行读入两个整数n，m，表示共n个点m条边。 接下来m行，每行三个正整数x，y，z，表示点x到点y有一条边权为z的边。

输出格式：

输出仅包括一行，记为所求路径的边权之积，由于答案可能很大，因此狗哥仁慈地让你输出它模9987的余数即可。

废话当然是一个数了w

//谢fyszzhouzj指正w

对于20%的数据，n<=10。

对于100%的数据，n<=1000，m<=1000000。边权不超过10000。

输入输出样例

输入样例#1：

3 3

1 2 3

2 3 3

1 3 10

输出样例#1：

9

说明

好好看一看再写哟w

题解

直接乘会爆，取对数把乘法改成加法即可，\(log_{ab} = log_a + log_b\)，讨论区说测试样例太弱了，不log，甚至不取模也能过，所以也不知道有没有效。

从评论区学到了新知识，快速乘。另文。

#include <algorithm>
#include <cmath>
#include <iostream>
#include <queue>
#include <vector>

using namespace std;

int n, m;

struct edge_t {
    int dst;
    int weight;
    double logw;
};

vector<edge_t> edges[1005];
int weight[1005][1005];

int main(void) {
#ifdef DEBUG
    freopen("in.txt", "r", stdin);
#endif

    cin >> n >> m;

    for (int i = 0; i < m; ++i) {
        int src;
        edge_t e;
        cin >> src >> e.dst >> e.weight;
        e.logw = log(e.weight);
        weight[src][e.dst] = weight[e.dst][src] = e.weight;

        edges[src].push_back(e);
    }

    queue<int> que;
    que.push(1);

    vector<bool> vis(n+1);
    fill(vis.begin(), vis.end(), false);
    vis[1] = true;

    vector<double> dist(n+1);
    fill(dist.begin(), dist.end(), 999999);
    dist[1] = 0;

    vector<int> pre(n+1);

    while (!que.empty()) {
        int x = que.front();
        que.pop();
        vis[x] = false;

        for (vector<edge_t>::iterator it = edges[x].begin(); it != edges[x].end(); ++it) {
            if (dist[it->dst] > dist[x] + it->logw) {
                dist[it->dst] = dist[x] + it->logw;
#ifdef DEBUG
                cout << "[*] " << it->dst << endl;
#endif
                pre[it->dst] = x;

                if (!vis[it->dst]) {
                    vis[it->dst] = true;
                    que.push(it->dst);
                }
            }
        }
    }

    int ans = 1;
    for (int x = n; pre[x]; x = pre[x]) {
        ans *= weight[x][pre[x]];
        ans %= 9987;
    }

    cout << ans;
}

这次代码比上一题要工好多。越晚越精神？