BZOJ 3156: 防御准备 斜率优化DP

3156: 防御准备

Description

 

Input

第一行为一个整数N表示战线的总长度。

第二行N个整数，第i个整数表示在位置i放置守卫塔的花费Ai。

Output

共一个整数，表示最小的战线花费值。

Sample Input

10
2 3 1 5 4 5 6 3 1 2

Sample Output

18

HINT

1<=N<=10^6,1<=Ai<=10^9

题解：

　　斜率优化DP；

　　首先将数组倒置

　　设定dp[i] 为前i的点的最优答案

　　易得

　　　　dp[i] = min{dp[j]+(i-j-1)*(i-j)/2}+a[i]; 1<=j<i;

　　

　　

　　

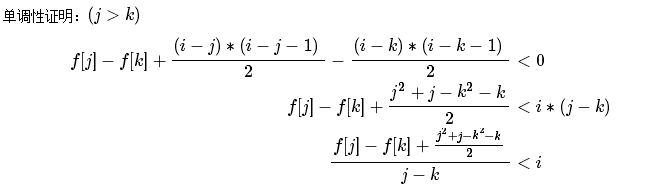
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e6+,inf = 2e9, mod = 1e9+;
typedef long long ll;

ll dp[N];
ll n,a[N],b[N];
double getsum(ll k,ll j)
{
    return (double)((dp[k]-dp[j]) + (double)(k*k+k-j*j-j)/2.0)/(double)(k-j);
}
int main()
{
    scanf("%lld",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%lld",&b[i]);
    }
    for(int i=;i<=n;i++)
    {
        a[i]=b[n-i+];
    }
    deque<int > q;
    dp[] = a[];
    q.push_back();
    for(int i=;i<=n;i++)
    {
        int now=q.front();q.pop_front();
        while(!q.empty()&&getsum(q.front(),now)<i) now=q.front(),q.pop_front();
        q.push_front(now);
        dp[i] = dp[now] + (ll)(i-now-)*(ll)(i-now)/ + a[i];
        now = q.back();q.pop_back();
        while(!q.empty()&&getsum(i,now)<getsum(now,q.back())) now=q.back(),q.pop_back();
        q.push_back(now);
        q.push_back(i);
    }
    ll ans=1e18;
    for(int i=;i<=n;i++)
        ans=min(ans,dp[i]+(ll)(n-i)*(n-i+)/);
    printf("%lld\n",ans);

    return ;
}