一步一步分析HTTPS加密机制

HTTPS（SSL/TLS）的加密机制虽然是大家都应了解的基本知识, 但是更多的时候我们只是在背诵一些概念, 比如: "对称加密", "非对称加密", "数字证书". 但是我们很少去思考 "为什么". 本文围绕 "为什么" 展开, 一步一步解开 HTTPS 的面纱.

为什么要加密?

因为http的内容是明文传输的，明文数据会经过中间代理服务器、路由器、wifi热点、通信服务运营商等多个物理节点，如果信息在传输过程中被劫持，传输的内容就完全暴露了。劫持者还可以篡改传输的信息且不被双方察觉，这就是中间人攻击。所以我们才需要对信息进行加密。最容易理解的就是对称加密。

什么是对称加密?

对称加密的要点是: 加密和解密只需要1个秘钥

下面是对称加密的伪代码

密文 = encode(明文, 秘钥)

明文 = decode(密文, 秘钥)

对称加密的步骤是什么?

对称加密的步骤如下:

小明和小红协商一个秘钥
小明使用秘钥加密数据, 发送密文
小红使用秘钥解密密文, 得到明文

对称加密示例-简单替换密码

简单替换密码系统中，我们为26个字母建立映射关系，例如s->a、c->d、h->n、o->x、l->y…… 26个字母被影射为另外的字母，那么一个明文的单词被加密后就无法认出了。例如school，按照上面的映射关系，就变成了adnxxy。

在这个密码系统中也存在密码算法和密钥。

密码算法：26个字母按照固定的映射关系做替换
密钥：26个字母的替换关系

如果想要破解密钥，也就是要找出26个字母的替换关系。a有26种替换可能，b有除a选择替换的字母之外的25种可能。以此类推，存在的替换关系有26x25x24……x1,约为2的88次方。如果计算机可以一秒尝试一亿个密码，运气差的话要尝试1200亿年。因此暴力破解是行不通的。

但是由于密码算法中，替换关系是稳定的，所以可以采用频率分析的方式破解密码。原理是明文中同一个字母出现的频率和密文中被替换的字母出现的频率一致。在英文中，字母出现的频率是相对稳定的。因此可以根据字母出现的频率推算出替换关系，也就是密钥。从而完成破解。

由此可见这种密码系统不安全的根源在于密码算法，该算法很容易让破解者推测出密钥，因此安全性极低。

对称加密示例-AES

AES 示例比较复杂, 是生产环境中常用的加密算法, 可以考虑跳过该部分

AES（advanced encryption standard）算法是经过公开选拔所产生。这样彻底杜绝了 "隐蔽式安全性"。最终，比利时密码学家 Joan Daemen 和 Vincent Rijme 开发的密码算法 Rijndael成为了 AES 标准。

AES 所支持的 Rijndael 密码算法，分组长度为 128 比特，密钥长度有 128、192、256比特三种选择。

AES 算法也有多个轮次，每轮次有如下四个步骤：

SubBytes
ShiftRows
MixColumns
AddRoundKey

SubBytes:

类似于简单替换，将每个字节的值替换为另外的值。

ShiftRows:

首先将明文以4字节为一行，转化为多行，也就是矩阵。每行按照一定规则向左平移

MixColumns:

将矩阵的列，每4个字节为单位进行比特运算，转化为另外的4字节值。

AddRoundKey:

将 MixColumns 后的数据与轮密钥进行 XOR 运算。

以上四步执行完后，一轮 Rijndael 加密就结束了。Rijndael 加密一般要进行 10-14 轮计算。

Rijndael 解密的过程则是相反的顺序：

AddRoundKey
MixColumns
ShiftRows
SubBytes

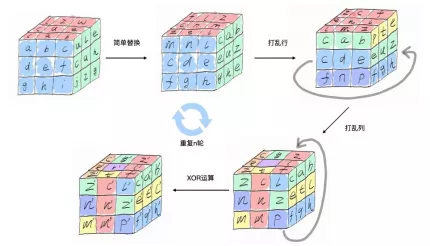
Rijndael 加密的过程有点像玩魔方。假如有种魔方，除了和普通魔方相同之处外，每个格子还写有文字。Rijndael 加密的过程和打乱这个魔方非常像。横着转几下，竖着转几下。除了打乱行、列，还对格子里的值做了替换以及 XOR 加密。

而 Rijndael 解密的过程就是还原魔方，只不过不但颜色要还原一致，魔方格子上的文字也要还原。你是否担心会玩魔方的人很容易就能复原？由于AES中使用了密钥，所以即使精通AES算法，拿不到密钥也很难还原。

切记不要试图自己开发加密算法，通过隐藏加密算法的方式来提高安全性。要杜绝隐蔽式安全性。没有特殊情况，我们都应该首选 AES。

对称加密问题是什么?

对称加密的问题在于第一步: 协商秘钥

如果小明将将秘钥发送给小红, 黑客就可以在网络线路上截获秘钥, 这样黑客就可以解密所有的数据了

有如下几种解决密钥配送问题的方案：

事先共享密钥: 比如小明和小红私下交换秘钥
密钥分配中心: 比如小明和小红将秘钥发送给密钥分配中心, 然后密钥分配中心将秘钥发送给小明和小红
非对称加密

下面主要介绍一种解决方案: 非对称加密

什么是非对称加密?

非对称加密的要点是: 加密和解密需要2个秘钥

公钥加密数据, 私钥解密数据

非对称加密的伪代码如下:

密文 = encode(明文, 公钥)

明文 = decode(密文, 私钥)

注意CA机构是相反的: 私钥签名, 公钥验证签名

非对称加密的密码学实现比较复杂, 这里不赘述

非对称加密的步骤是什么?

一共4个秘钥,小红有私钥和公钥, 小明有私钥和公钥

小明将公钥发送给小红, 小红将公钥发送给小明
小红使用小明的公钥加密数据, 发送密文
小明使用自己的私钥解密密文, 得到明文

非对称加密的效率问题?

非对称加密算法非常耗时，而对称加密快很多, 一般的方案是: 使用非对称加密算法交换对称加密的密钥, 然后使用对称加密算法加密数据

非对称加密的安全问题?

黑客无法获取内容, 但是黑客可以拦截伪造

小明和小红的公钥都在网络中传输过, 黑客就可以在网络线路上截获公钥和密文, 但是黑客没有私钥, 黑客无法解密内容

但是黑客可以拦截伪造

比如小明登录网站, 黑客拦截了小明对网站的登录请求, 然后黑客将自己的公钥发给了小明, 小明用黑客的公钥加密了账号和密码发给了黑客, 黑客用自己的私钥解密, 就获得了小明的账号密码

所以 你怎么鉴别别人给你的公钥是对的?

下面介绍一种解决方案: 证书

证书是什么?

证书解决公钥的信任问题, 由权威机构告诉你你手上的公钥是这个网站的, 而不是黑客伪造的

请记住一句话: 公钥加密，私钥解密；私钥签名，公钥验签

证书的步骤是什么?

网站生成网站公钥和网站私钥
网站将自己的公钥(明文数据)交给权威机构认证(一般是域名的管理员才能通过认证)
CA机构对证书明文数据T进行hash
CA机构对hash后的值用私钥加密(不同之处在于CA机构用私钥加密, 公钥解密)，得到数字签名S, 证书=明文数据+数字签名
用户下载的浏览器都默认安装了主流CA机构的公钥, 用户从网站下载证书后通过机构公钥解密证书的签名, 然后对证书明文数据进行hash, 如果hash值和签名一致, 证明证书是CA机构签发的, 证书是可信的.
用户通过网站的公钥(也就是证书中的明文数据), 对明文进行加密, 发送密文
网站通过自己的私钥对密文进行解密, 得到明文

总之就是: 通过加了一层机构来保证公钥的正确性

为什么CA机构对明文加密前要先hash?

如果直接对明文加密, 会很慢, 所以先对明文进行hash, 然后对hash值进行加密, 这样速度会快很多

机构是干嘛的?

机构的工作主要就是认证证书的生成和管理

生成证书

负责认申请人的身份, 一般是域名所有人, 认证通过后生成证书

管理证书

如果网站的私钥被泄露了, 网站需要将改证书作废, 重新生成新的证书

机构是哪个国家的?

权威机构有几个公司, 浏览器默认都安装了他们的公钥, 大部分都是美国的

跟域名, IP地址一样, CA证书也是互联网的资源, 可以用来卡脖子.

有一个知乎问答: 西方机构吊销了俄罗斯的HTTPS证书有什么影响吗？https://www.zhihu.com/question/523817733/answer/2440936723

如果黑客伪造了机构的的证书呢?

我们怎么知道机构一定是可信任的呢, 我们应该信任哪家机构呢, 如果黑客伪造了机构的的证书呢?

核心要点是: 我们最终选择相信根CA

浏览器内置了一些根CA, 一般是国家级的机构, 比如: Verisign, Thawte, GeoTrust, Comodo, DigiCert, Entrust, GlobalSign, GoDaddy, Network Solutions, Symantec, etc.
根CA可以给及其他机构或者网站颁发证书
其他机构可以给其他机构或者网站颁发证书
但是最终一定是能追溯到根CA, 我们默认根CA是可靠的(只要浏览器软件是可靠的, 不要下盗版的软件, 另外我们也可以自己安装CA到设备中)

你仍旧不信任根 CA？抱歉，你也只能信任根CA。

HTTPS是什么?

上面介绍了, 对称加密, 非对称加密, 证书. 把它们结合起来, 解决效率和安全性的问题, 这就是 https

参考资料: https://blog.csdn.net/odyyy/article/details/80256129

reference

密码学: https://icodebook.com/

HTTPS: https://zhuanlan.zhihu.com/p/43789231

CA，证书，公钥，私钥，加密算法常识总结: https://www.cnblogs.com/yb38156/p/14293382.html