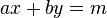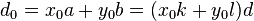as+bt=1是ab两数互质的充要条件
【as+bt=1是ab两数互质的充要条件】
充分性,as+bt=1 => (a,b)=1:
因为as+bt=1,设c=(a,b),则c整除a和b,所以c整除as+bt,即c整除1,所以c=1,即a和b互质
必要性,(a,b)=1 => ab+bt=1:
考虑非空集合A={as+bt│s,t为任意整数},不妨设a0是A中最小正整数且a0=as0+bt0,y是A中任意一个元素,
由带余除法 y=as+bt=q(as0+bt0)+r,0<=r<a0,则r=a(s-qs0)+b(t-qt0)属于A,若r非零则r是A中比a0更小之正整数,矛盾,所以r=0,从而a0整除y。
因为a0整除y,所以 (as+bt)/a0 = q。=> as/a0+bt/a0 = q。s、t为任意值,而q必然为整数,则as/a0、bt/a0必须是整数。则有a0整除a,a0整除b,所以a0整除(a,b)=1,因此a0=1,所以存在整数s0和t0使得as0+bt0=1
【贝祖定理(裴蜀定理)】
有整数解时当且仅当m是d的倍数。d是(a,b)。裴蜀等式有解时必然有无穷多个整数解,每组解 、
、 都称为裴蜀数。在前部分证明的基础上,
都称为裴蜀数。在前部分证明的基础上,
对  和
和  的任意正公约数
的任意正公约数 ,设
,设 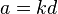 、
、 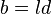 ,那么
,那么
因此 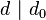 。所以
。所以  是
是  和
和  的最大公约数。
的最大公约数。
参考:http://zh.wikipedia.org/wiki/%E8%B2%9D%E7%A5%96%E7%AD%89%E5%BC%8F
as+bt=1是ab两数互质的充要条件的更多相关文章
- hdu 5072 两两(不)互质个数逆向+容斥
http://acm.hdu.edu.cn/showproblem.php?pid=5072 求n个不同的数(<=1e5)中有多少组三元组(a, b, c)两两不互质或者两两互质. 逆向求解,把 ...
- 洛谷题解 P1592 【互质】
原题传送门 题目描述 输入两个正整数n和k,求与n互质的第k个正整数. 输入格式 仅一行,为两个正整数n(≤10^6)和k(≤10^8). 输出格式 一个正整数,表示与n互质的第k个正整数. 输入输出 ...
- 欧拉函数(小于或等于n的数中与n互质的数的数目)&& 欧拉函数线性筛法
[欧拉函数] 在数论,对正整数n,欧拉函数是少于或等于n的数中与n互质的数的数目.此函数以其首名研究者欧拉命名,它又称为Euler’s totient function.φ函数.欧拉商数等. 例如φ( ...
- openjudge7834:分成互质组 解析报告
7834:分成互质组 总时间限制: 1000ms 内存限制: 65536kB 描述 给定n个正整数,将它们分组,使得每组中任意两个数互质.至少要分成多少个组? 输入 第一行是一个正整数n.1 &l ...
- poj3696 快速幂的优化+欧拉函数+gcd的优化+互质
这题满满的黑科技orz 题意:给出L,要求求出最小的全部由8组成的数(eg: 8,88,888,8888,88888,.......),且这个数是L的倍数 sol:全部由8组成的数可以这样表示:((1 ...
- HDU5668 Circle 非互质中国剩余定理
分析:考虑对给定的出圈序列进行一次模拟,对于出圈的人我们显然可以由位置,编号等关系得到一个同余方程 一圈做下来我们就得到了n个同余方程 对每个方程用扩展欧几里得求解,最后找到最小可行解就是答案. 当然 ...
- 51 nod 1419 最小公倍数挑战【数论/互质+思维】
1419 最小公倍数挑战 题目来源: CodeForces 基准时间限制:1 秒 空间限制:131072 KB 分值: 40 难度:4级算法题 收藏 关注 几天以前,我学习了最小公倍数.玩得挺久了 ...
- 用python实现了一下:甲乙两人互猜数字(数理逻辑)
今天在园子里看到博客:超难面试题:甲乙两人互猜数字(数理逻辑).然后琢磨了半天,写了个Python程序实现算法,我得出来的结果是1,6或1,8或35,42的组合, 不知道是否正确,请高人指点? 下面列 ...
- LeetCode 29 - 两数相除 - [位运算]
题目链接:https://leetcode-cn.com/problems/divide-two-integers/description/ 给定两个整数,被除数 dividend 和除数 divis ...
随机推荐
- windows 改路径有小差异
https://jingyan.baidu.com/article/5552ef473e2df6518ffbc916.html cmd是windows下一个非常常用的工具,但是它默认的地址却是不变的. ...
- Electron中git, npm,webpack使用
开始学习Electron的时候用到git, 记录学习一下, 学习地址是: https://zhuanlan.zhihu.com/p/20225295?columnSlug=FrontendMagazi ...
- Java8新特性Optional、接口中的默认方法与静态方法
Optional Optional 类(java.util.Optional) 是一个容器类,代表一个值存在或不存在,原来用 null 表示一个值不存在,现在 Optional 可以更好的表达这个概念 ...
- html中<video>显示视频的时候,MP4的格式问题
html支持的视频格式:HTML5视频 注意 浏览器对mp4 的编码方式要求的非常严格 视频编码必须是H.264 音频编码必须是: AAC
- 【工作】to-do-list
当你不确定的时候,你就把你所在的工作做好,所在的你不愿意的行业做好,所谓的自由选择,它本身不自由的,不自由过程当中,如何你把它做好,就做人生的一个经历,人生的一个积累.-- 王石 TODO
- Django-rest-framework多条件查询/分页/多表Json
http://www.mamicode.com/info-detail-1648765.html
- css关系选择符
<!Doctype html> <html> <head> <meta http-equiv="Content-Type" content ...
- 在TreeView 控件上,如果双击任何一个节点的checkbox 只会收到一次After_Check事件 但是check属性变化两次(从false到true 再从true到false),请问该如何解决,谢谢!
在TreeView 控件上,如果双击任何一个节点的checkbox 只会收到一次After_Check事件 但是check属性变化两次(从false到true 再从true到false),请问该如何解 ...
- 一键获取 所有连接过的WIFI密码
使用方法 一.运行CMD (以及 开启无线网卡.最好是笔记本) 二.输入命令: for /f "skip=9 tokens=1,2 delims=:" %i in ('netsh ...
- 借助curl理解$GLOBALS['HTTP_RAW_POST_DATA'] ,$_POST, php://input
发送请求代码 post.php <?php $url='http://localhost/web/curl/url.php'; $data='a=123|b=2&c=3'; $heade ...