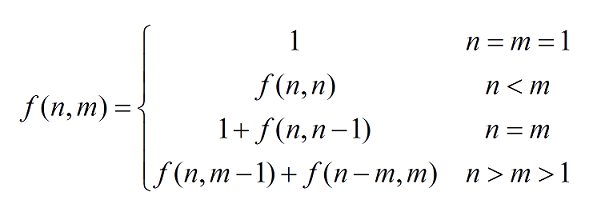某dp题
【NOI联考by ysy】庆典
2016年6月17日1,1040
【题目描述】
战狂在昌和帝国的首都法法城召开了庆典,向一万名最杰出的士兵分发了用魔法猪做的猪肉饺子,士兵们吃了猪肉饺子后,战斗力大幅提高。
为了保护战狂的安全以及维护现场秩序,大预言家抽调了n名普通士兵组成了m个小队完成一些不同的任务。由于一些特殊的原因,所有小队的人数都互不相同。
你需要求出有多少种可能的组队方案。注意士兵是相同的,而小队是不同的。
【输入数据】
第一行两个个整数n,m。
【输出数据】
一行一个数表示答案。对998244353取模。
【样例输入】
16 4
【样例输出】
216
【数据范围】
对于20%的数据,n,m<=20。
对于50%的数据,n,m<=3000。
对于100%的数据,n,m<=100000。
这个题目就比较简单
首先所有小队的人都不相同
那就先给每个位置\(i\)分配\(i\)个队员
对于剩下的人就分配给这m个小队
所以就\(O(nm)\)递推
这个递推有点熟悉(整数拆分问题)
递推法
根据n和m的关系,考虑下面几种情况:
(1)当n=1时,不论m的值为多少(m>0),只有一种划分,即\({1}\);
(2)当m=1时,不论 的值为多少(n>0),只有一种划分,即\({1,1,....1,1,1}\);
(3)当n=m时,根据划分中是否包含n,可以分为两种情况:
(a)划分中包含n的情况,只有一个,即\({n}\);
(b)划分中不包含n的情况,这时划分中最大的数字也一定比n小,即n的所有\((n-1)\)划分;
因此,\(f(n,n)=1+f(n, n-1)\)。
(4)当n时,由于划分中不可能出现负数,因此就相当于f(n,n);
(5)当n>m时,根据划分中是否包含m,可以分为两种情况:
(a)划分中包含 的情况,即{m,{x1,x2,x3,...,xi}},其中{x1,x2,x3,...,xi}的和为n-m,可能再次出现m,因此是(n-m)的m划分,因此这种划分个数为f(n-m,m;
(b)划分中不包含m的情况,则划分中所有值都比m小,即n的(m-1)划分,个数为f(n,m-1;
因此,f(n,m)=f(n-m,m)+f(n,m-1) 。
综合以上各种情况,可以看出,上面的结论具有递归定义的特征,其中(1)和(2)属于回归条件,(3)和(4)属于特殊情况,而情况(5)为通用情况,属于递归的方法,其本质主要是通过减少n或m以达到回归条件,从而解决问题。
详细递推公式描述如下:
那么
#include<iostream>
#include<cstdio>
#define N 100005
#define mod 998244353
using namespace std;
int dp[N];
int main(){
int n,m;
cin>>n>>m;
n-=m*(m+1)/2;
dp[0]=1;
for(int i=1;i<=m;++i)
for(int j=i;j<=n;++j)
dp[j]=(dp[j]+dp[j-i])%mod;
for(int i=2;i<=m;++i)
dp[n]=(dp[n]*i)%mod;
printf("%d",dp[n]);
return 0;
}
某dp题的更多相关文章
- Codeforces Round #369 (Div. 2)---C - Coloring Trees (很妙的DP题)
题目链接 http://codeforces.com/contest/711/problem/C Description ZS the Coder and Chris the Baboon has a ...
- 4817 江哥的dp题d
4817 江哥的dp题d 时间限制: 1 s 空间限制: 256000 KB 题目等级 : 黄金 Gold 题解 题目描述 Description 已知1-N的排列P的LIS(最长上 ...
- 4809 江哥的dp题c
4809 江哥的dp题c 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 黄金 Gold 题解 题目描述 Description 有两个数x,y,一开始x=1,y= ...
- 4816 江哥的dp题b
4816 江哥的dp题b 时间限制: 1 s 空间限制: 256000 KB 题目等级 : 黄金 Gold 题解 题目描述 Description 给出两个1-N的随机排列A,B.若 ...
- 4815 江哥的dp题a
4815 江哥的dp题a 时间限制: 1 s 空间限制: 256000 KB 题目等级 : 黄金 Gold 题解 题目描述 Description 给出一个长度为N的序列A(A1,A ...
- HDU 2577 How to Type(dp题)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2577 解题报告:有一个长度在100以内的字符串,并且这个字符串只有大写和小写字母组成,现在要把这些字符 ...
- codevs4817 江哥的dp题d
4817 江哥的dp题d 时间限制: 1 s 空间限制: 256000 KB 题目等级 : 黄金 Gold [题目描述] Description 已知1-N的排列P的LIS(最长上升子序列)不超 ...
- 古韵之乞巧 题解 dp题
[noip模拟赛1]古韵之乞巧 描述 闺女求天女,更阑意未阑. 玉庭开粉席,罗袖捧金盘. 向月穿针易,临风整线难. 不知谁得巧,明旦试相看. ——祖咏<七夕> 女子乞巧,是七夕的重头戏 ...
- cf1061c 普通dp题
题解见https://blog.csdn.net/godleaf/article/details/84402128 这一类dp题是可以压缩掉一维空间的,本题枚举a1到an,枚举到ai时枚举ai的每个约 ...
- HDU 4472 Count DP题
解题报告:题目大意,给你n个球,要将这n个球从下到上按层次排列,要求同一个层次的的每一个分支的数量都必须相等,问有多少种排列的方法. 此题的一个DP题,假设现在有n个球,要将这n个球排列好,我们就必须 ...
随机推荐
- struts2中的action为什么要继承ActionSupport类,不继承也可以,有什么好处?
简单来说,有很多相关的方法都加载进来,你直接调用就行了,而且在安全上和稳定性上做了很好的处理 实际上继承ActionSupport之后 就等同于实现了很多接口 Action,Validateable, ...
- sql声明变量存储查询结果
with t as 查到条件数据,然后在下面使用到t,用exists做判断会非常慢,改成left join会快很多. 我使用的数据库时2008Sql r2. 文章:SQL数据库中临时表.临时变量和WI ...
- lintcode-74-第一个错误的代码版本
74-第一个错误的代码版本 代码库的版本号是从 1 到 n 的整数.某一天,有人提交了错误版本的代码,因此造成自身及之后版本的代码在单元测试中均出错.请找出第一个错误的版本号. 你可以通过 isBad ...
- 并发(一) Semaphore
Semaphore 控制对资源的并发访问数,构造时如果传参为1,则近似于ReentrantLock,差别在于锁的释放.可以一个线程获取锁,另外一个线程释放锁,在一些死锁处理的场合比较适用. 如上所示, ...
- spring笔记(二)
共性问题: 1. 服务器启动报错,什么原因? * jar包缺少.jar包冲突 1) 先检查项目中是否缺少jar包引用 2) 服务器: 检查jar包有没有发布到服务器下: 用户库jar包,需要手动发布到 ...
- MongoDB 存储日志数据
MongoDB 存储日志数据 https://www.cnblogs.com/nongchaoer/archive/2017/01/11/6274242.html 线上运行的服务会产生大量的运行及访问 ...
- BZOJ4476 送礼物
这道题真是有趣呀. 其实就是一个分数规划问题,用一个二分加log来得去掉分母. 分四种情况讨论 1.lenth > L && num ( max ) > num ( min ...
- GDB使用小记
By francis_hao Nov 7,2016 记录GDB常用功能. GDB可以让你查看一个程序在运行时其内部发生了什么,或者当一个程序崩溃时发生了什么(通过使用GDB查看core dum ...
- [hdu 3652]数位dp解决数的倍数问题
原以为很好的理解了数位dp,结果遇到一个新的问题还是不会分析,真的是要多积累啊. 解决13的倍数,可以根据当前余数来推,所以把当前余数记为一个状态就可以了. #include<bits/stdc ...
- POJ2195:Going Home (最小费用最大流)
Going Home Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 26212 Accepted: 13136 题目链接 ...