hdu 3870（平面图最小割转最短路）

Catch the Theves

Time Limit: 5000/2000 MS (Java/Others)    Memory Limit: 65768/32768 K (Java/Others)
Total Submission(s): 1640    Accepted Submission(s): 514

Problem Description

A
group of thieves is approaching a museum in the country of zjsxzy,now
they are in city A,and the museum is in city B,where keeps many broken
legs of zjsxzy.Luckily,GW learned the conspiracy when he is watching
stars and told it to zjsxzy.
Zjsxzy decided to caught these
thieves,and he let the police to do this,the police try to catch them on
their way from A to B. Although the thieves might travel this way by
more than one group, zjsxzy's excellent police has already gather the
statistics that the cost needed on each road to guard it.
Now
,zjsxzy's conutry can be described as a N*N matrix A,Aij indicates the
city(i,j) have bidirectionals road to city(i+1,j) and city(i,j+1),gurad
anyone of them costs Aij.
Now give you the map,help zjsxzy to
calculate the minimium cost.We assume thieves may travel in any way,and
we will catch all passing thieves on a road if we guard it.

 

Input

The first line is an integer T,followed by T test cases.
In each test case,the first line contains a number N(1<N<=400).
The following N lines,each line is N numbers,the jth number of the ith line is Aij.
The city A is always located on (1,1) and the city B is always located on (n,n).
Of course,the city (i,j) at the last row or last line won't have road to (i,j+1) or (i+1,j).

 

Output

For each case,print a line with a number indicating the minimium cost to arrest all thieves.

 

Sample Input

1
3
10 5 5
6 6 20
4 7 9

 

Sample Output

18

Hint

The map is like this: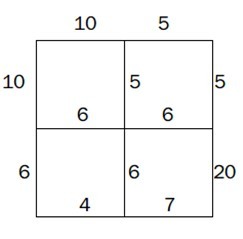

 

Source

2011 Multi-University Training Contest 4 - Host by SDU

 

 

题意:从左上角走到右下角的方案数.

题解:一看以为是最小割,但是点有1600000个，显然不现实,其实刘汝佳书里面有个类似的题，，不过没看懂方法。。然后到网上找题解,,发现构造对偶图然后求解对偶图的最短路。。好神奇

http://blog.csdn.net/ahero_happy/article/details/6637214

#include <iostream>
#include <cstdio>
#include <string.h>
#include <queue>
#include <algorithm>
#include <math.h>
using namespace std;
typedef long long LL;
const int INF = ;
const int N = ;
const int M = N*N;
int a[N][N];
struct Edge{
    int v,w,next;
}edge[*M];
int head[M];
int tot,n;
void addEdge(int u,int v,int w,int &k){
    edge[k].v = v,edge[k].w = w,edge[k].next = head[u],head[u] = k++;
}
void init(){
    memset(head,-,sizeof(head));
    tot = ;
}
bool vis[M];
int low[M];
int spfa(int s,int t){
    for(int i=;i<=t;i++){
        low[i] = INF;
        vis[i] = false;
    }
    low[s] = ;
    queue<int> q;
    q.push(s);
    while(!q.empty()){
        int u = q.front();
       // printf("%d\n",u);
        q.pop();
        vis[u] = false;
        for(int k = head[u];k!=-;k = edge[k].next){
            int v = edge[k].v,w=edge[k].w;
           // printf("%d %d\n",v,w);
            if(low[v]>low[u]+w){
                low[v] = low[u]+w;
                if(!vis[v]){
                    vis[v] = true;
                    q.push(v);
                }
            }
        }
    }
    return low[t];
}
int main(){
    int tcase;
    scanf("%d",&tcase);
    while(tcase--){
        init();
        scanf("%d",&n);

        for(int i=;i<=n;i++){
            for(int j=;j<=n;j++){
                scanf("%d",&a[i][j]);
            }
        }
        n-=;
        int s = ,t = n*n+;
        /**构造对偶图*/
        for(int i=;i<=n;i++){
            for(int j=;j<=n;j++){
                int now = (i-)*n+j;
                int next1 = (i-)*n+j+;
                int next2 = (i-)*n+j+n;
                if(j!=n) {
                    addEdge(now,next1,a[i][j+],tot);
                    addEdge(next1,now,a[i][j+],tot);
                }
                if(i!=n){
                    addEdge(now,next2,a[i+][j],tot);
                    addEdge(next2,now,a[i+][j],tot);
                }
                if(j==){
                    addEdge(s,now,a[i][j],tot);
                    addEdge(now,s,a[i][j],tot);
                }
                if(i==n){
                    addEdge(s,now,a[i+][j],tot);
                    addEdge(now,s,a[i+][j],tot);
                }
                if(i==){
                    addEdge(t,now,a[i][j],tot);
                    addEdge(now,t,a[i][j],tot);
                }
                if(j==n){
                    addEdge(t,now,a[i][j+],tot);
                    addEdge(now,t,a[i][j+],tot);
                }
            }
        }
        printf("%d\n",spfa(s,t));
    }
    return ;
}