电路维修（双端队列 & 最短路）

达达是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女翰翰，从而被收留在地球上。

翰翰的家里有一辆飞行车。

有一天飞行车的电路板突然出现了故障，导致无法启动。

电路板的整体结构是一个$R$行$C$列的网格（R,C≤500），如下图所示。

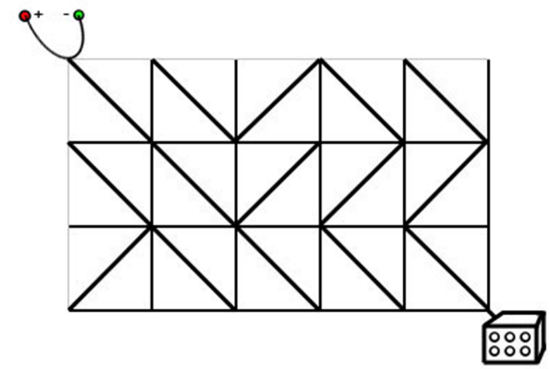
每个格点都是电线的接点，每个格子都包含一个电子元件。

电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。

在旋转之后，它就可以连接另一条对角线的两个接点。

电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

达达发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。

她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。

不过，电路的规模实在是太大了，达达并不擅长编程，希望你能够帮她解决这个问题。

输入格式

输入文件包含多组测试数据。

第一行包含一个整数T，表示测试数据的数目。

对于每组测试数据，第一行包含正整数R和C，表示电路板的行数和列数。

之后R行，每行C个字符，字符是"/"和"\"中的一个，表示标准件的方向。

输出格式

对于每组测试数据，在单独的一行输出一个正整数，表示所需的缩小旋转次数。

如果无论怎样都不能使得电源和发动机之间连通，输出NO SOLUTION。

---

emmmmm， 一道《算法进阶》上的题， 书中所给的方法是双端队列， 但身为蒟蒻的我怎么可能会，所以我想到了SPFA算法。

把每一个格点当做节点， 则共有（n + 1）* （m + 1）的节点， 在下图中， 就将1到4这条边的边权设为0， 而2到3这条边就为1，

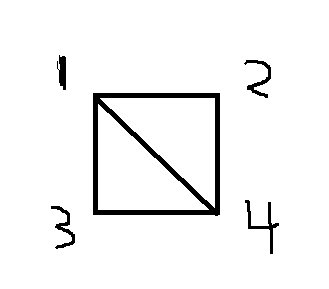
通过这样的建图， 我们以1为起点， 跑一边最短路，输出终点的距离即可，注意的是， 当终点的距离为无限大时， 即到达不了终点， 输出NO SOLUTION；

比较坑的是， 这道题的数据竟然卡SPFA， 所以用Dijkstra就行了

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + 100;
const int MAXM = 3e3 + 10;

template < typename T > inline void read(T &x) {
    x = 0; T ff = 1, ch = getchar();
    while(!isdigit(ch)) {
        if(ch == '-') ff = -1;
        ch = getchar();
    }
    while(isdigit(ch)) {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
    x *= ff;
} 

template < typename T > inline void write(T x) {
    if(x < 0) putchar('-'), x = -x;
    if(x > 9) write(x / 10);
    putchar(x % 10 + '0');
} 

int T, n, m;
int vis[MAXN], dis[MAXN];
int lin[MAXN], tot = 0;
char ch;
struct edge {
    int y, v, next;
}e[MAXN];

inline void add(int xx, int yy, int vv) {
    e[++tot].y = yy;
    e[tot].v = vv;
    e[tot].next = lin[xx];
    lin[xx] = tot;
}

/*void SPFA() {
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, false, sizeof(vis));
    queue < int > q;
    q.push(1);
    dis[1] = 0;
    while(!q.empty()) {
        int x = q.front(); q.pop(); vis[x] = false;
        for(int i = lin[x], y; i; i = e[i].next) {
            if(dis[y = e[i].y] > dis[x] + e[i].v) {
                dis[y] = dis[x] + e[i].v;
                if(!vis[y]) {
                    vis[y] = true;
                    q.push(y);
                }
            }

        }
    }

}*/

void Dijkstra() {
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, false, sizeof(vis));
    priority_queue < pair < int, int > > q;
    dis[1] = 0;
    q.push(make_pair(0, 1));
    while(!q.empty()) {
        int x = q.top().second; q.pop();
        if(vis[x]) continue;
        vis[x] = true;
        for(int i = lin[x], y; i; i = e[i].next) {
            if(dis[y = e[i].y] > dis[x] + e[i].v) {
                dis[y] = dis[x] + e[i].v;
                if(!vis[y]) q.push(make_pair(-dis[y], y));
            }
        }
    }
}

int main() {
    read(T);
    while(T--) {
        read(n); read(m);
        memset(lin, 0, sizeof(lin));
        memset(e, 0, sizeof(e));
        tot = 0;
        for(int i = 1; i <= n; ++i) {
            for(int j = 1; j <= m; ++j) {
                ch = getchar();
                if(ch == '/') {
                    add(((i - 1) * (m + 1) + j), i * (m + 1) + j + 1, 1);
                    add(i * (m + 1) + j + 1, (i - 1) * (m + 1) + j, 1);
                    add(i * (m + 1) + j, (i - 1) * (m + 1) + j + 1, 0);
                    add((i - 1) * (m + 1) + j + 1, i * (m + 1) + j, 0);
                }
                else {
                    add(((i - 1) * (m + 1) + j), i * (m + 1) + j + 1, 0);
                    add(i * (m + 1) + j + 1, (i - 1) * (m + 1) + j, 0);
                    add(i * (m + 1) + j, (i - 1) * (m + 1) + j + 1, 1);
                    add((i - 1) * (m + 1) + j + 1, i * (m + 1) + j, 1);
                }
            }
            ch = getchar();
        }
//        SPFA();
        Dijkstra();
        if(dis[(n + 1) * (m + 1)] == INF) puts("NO SOLUTION");
        else write(dis[(n + 1) * (m + 1)]), puts("");
    }
    return 0;
}

---

今天， 某位机房大佬教了我双端队列， 思想大概和我上面的相同， 也是建一条0或1的边， 只是在搜索的过程中，将边权为0的加入队头， 1加入队尾， 这样每个节点可能多次入队， 但第一次弹出时就是最短距离

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int INF = 0x3f3f3f3f;
const int MAXN = 5e5 + 100;
const int MAXM = 3e3 + 10;

template < typename T > inline void read(T &x) {
    x = 0; T ff = 1, ch = getchar();
    while(!isdigit(ch)) {
        if(ch == '-') ff = -1;
        ch = getchar();
    }
    while(isdigit(ch)) {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
    x *= ff;
}

template < typename T > inline void write(T x) {
    if(x < 0) putchar('-'), x = -x;
    if(x > 9) write(x / 10);
    putchar(x % 10 + '0');
}

int n, m, t;
int dis[MAXM][MAXM];
char ch[MAXM][MAXM];

int BFS() {
    deque < pair < int, int > > q;
    int dx[5] = {-1, -1, 1, 1}, dy[5] = {-1, 1, 1, -1};
    int ix[5] = {-1, -1, 0, 0}, iy[5] = {-1, 0, 0, -1};
    memset(dis, 0x3f, sizeof(dis));
    q.push_back(make_pair(0, 0));
    dis[0][0] = 0;
    char s[6] = "\\/\\/";
    while(!q.empty()) {
        pair < int, int > c = q.front();
        q.pop_front();
        int x = c.first, y = c.second;
        for(int i = 0; i < 4; ++i) {
            int u = x + dx[i], v = y + dy[i];
            int a = x + ix[i], b = y + iy[i];
            if(u > n || u < 0 || v > m || v < 0) continue;
            int w = 0;
            if(ch[a][b] != s[i]) ++w;
            if(dis[u][v] > dis[x][y] + w) {
                dis[u][v] = dis[x][y] + w;
                if(w) q.push_back(make_pair(u, v));
                else q.push_front(make_pair(u, v));
            }
        }
    }
    return dis[n][m];
}

int main() {
    read(t);
    while(t--) {
        read(n); read(m);
        for(int i = 0; i < n; ++i)
            scanf("%s", &ch[i]);
        int x = BFS();
        if(x == INF) puts("NO SOLUTION");
        else write(x), puts("");
    }
    return 0;
}