cf590A Median Smoothing

A. Median Smoothing

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A schoolboy named Vasya loves reading books on programming and mathematics. He has recently read an encyclopedia article that described the method of median smoothing (or median filter) and its many applications in science and engineering. Vasya liked the idea of the method very much, and he decided to try it in practice.

Applying the simplest variant of median smoothing to the sequence of numbers a1, a2, ..., an will result a new sequence b1, b2, ..., bnobtained by the following algorithm:

• b1 = a1, bn = an, that is, the first and the last number of the new sequence match the corresponding numbers of the original sequence.
• For i = 2, ..., n - 1 value bi is equal to the median of three values ai - 1, ai and ai + 1.

The median of a set of three numbers is the number that goes on the second place, when these three numbers are written in the non-decreasing order. For example, the median of the set 5, 1, 2 is number 2, and the median of set 1, 0, 1 is equal to 1.

In order to make the task easier, Vasya decided to apply the method to sequences consisting of zeros and ones only.

Having made the procedure once, Vasya looked at the resulting sequence and thought: what if I apply the algorithm to it once again, and then apply it to the next result, and so on? Vasya tried a couple of examples and found out that after some number of median smoothing algorithm applications the sequence can stop changing. We say that the sequence is stable, if it does not change when the median smoothing is applied to it.

Now Vasya wonders, whether the sequence always eventually becomes stable. He asks you to write a program that, given a sequence of zeros and ones, will determine whether it ever becomes stable. Moreover, if it ever becomes stable, then you should determine what will it look like and how many times one needs to apply the median smoothing algorithm to initial sequence in order to obtain a stable one.

Input

The first input line of the input contains a single integer n (3 ≤ n ≤ 500 000) — the length of the initial sequence.

The next line contains n integers a1, a2, ..., an (ai = 0 or ai = 1), giving the initial sequence itself.

Output

If the sequence will never become stable, print a single number  - 1.

Otherwise, first print a single integer — the minimum number of times one needs to apply the median smoothing algorithm to the initial sequence before it becomes is stable. In the second line print n numbers separated by a space  — the resulting sequence itself.

Sample test(s)

input

4
0 0 1 1

output

0
0 0 1 1

input

5
0 1 0 1 0

output

2
0 0 0 0 0

Note

In the second sample the stabilization occurs in two steps: 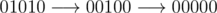, and the sequence 00000 is obviously stable.

比较恶心

很容易注意到对于一段连续的00或者11,他们下一步也一定是00或者11。

而对于每个ai,它的下一步取值跟ai-1,ai,ai+1有关，那么在00/11左边的和右边的是互不影响的。

于是我们可以认为每个00/11中间画一条线，把他们分开，像这样 0|0

于是序列被左右端点和这些我们画的“线”分成很多部分，答案就是这些区间的答案最大值

而这些区间又都没有连续的00或者11，那一定是0101010这样的

所以一段区间的答案只跟左右端点的值和区间长度有关

具体就很容易yy了

 #include<set>
 #include<map>
 #include<cmath>
 #include<ctime>
 #include<deque>
 #include<queue>
 #include<bitset>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #define LL long long
 #define inf 0x7fffffff
 #define pa pair<int,int>
 #define pi 3.1415926535897932384626433832795028841971
 using namespace std;
 inline LL read()
 {
     LL x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 int n,ans,l,a[],mrk;
 inline void jud(int l,int r)
 {
     if (l==r)return;
     if(a[l]==a[r])
     {
         for (int i=l;i<=r;i++)a[i]=a[l];
         ans=max(ans,(r-l)/);
         return;
     }else if (r-l>)
     {
         for (int i=l;i<=l+(r-l-)/;i++)a[i]=a[l];
         for (int i=r-(r-l-)/;i<=r;i++)a[i]=a[r];
         ans=max(ans,(r-l+)/-);
     }
 }
 int main()
 {
     n=read();for (int i=;i<=n;i++)a[i]=read();mrk=-;
     l=;
     for(int i=;i<=n;i++)
     {
         if (a[i]==mrk){l=i;continue;}
         mrk=-;
         if (i==n)jud(l,i);
         else if (a[i]==a[i-]&&i!=)jud(l,i-),l=i,mrk=a[i];

     }
     printf("%d\n",ans);
     for (int i=;i<=n;i++)printf("%d ",a[i]);
 }

cf590A