混沌分形之谢尔宾斯基（Sierpinski）

本文以使用混沌方法生成若干种谢尔宾斯基相关的分形图形。

（1）谢尔宾斯基三角形

给三角形的3个顶点，和一个当前点，然后以以下的方式进行迭代处理：

a.随机选择三角形的某一个顶点，计算出它与当前点的中点位置；

b.将计算出的中点做为当前点，再重新执行操作a

相关代码如下：

class SierpinskiTriangle : public FractalEquation
{
public:
    SierpinskiTriangle()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_triangleX[] = 0.0f;
        m_triangleY[] = FRACTAL_RADIUS;

        m_triangleX[] = FRACTAL_RADIUS*sinf(PI/);
        m_triangleY[] = -FRACTAL_RADIUS*sinf(PI/);

        m_triangleX[] = -m_triangleX[];
        m_triangleY[] = m_triangleY[];
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        int r = rand()%;
        outX = (x + m_triangleX[r])*0.5f;
        outY = (y + m_triangleY[r])*0.5f;
        outZ = z;
    }

private:
    float m_triangleX[];
    float m_triangleY[];
};

关于基类FractalEquation的定义见：混沌与分形

最终生成的图形为：

通过这一算法可以生成如下图像：

（2）谢尔宾斯基矩形

既然能生成三角形的图形，那么对于矩形会如何呢？尝试下吧：

class SierpinskiRectangle : public FractalEquation
{
public:
    SierpinskiRectangle()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_ParamA = 1.0f;
        m_ParamB = 1.0f;

        m_rectX[] = FRACTAL_RADIUS;
        m_rectY[] = FRACTAL_RADIUS;

        m_rectX[] = FRACTAL_RADIUS;
        m_rectY[] = -FRACTAL_RADIUS;

        m_rectX[] = -FRACTAL_RADIUS;
        m_rectY[] = -FRACTAL_RADIUS;

        m_rectX[] = -FRACTAL_RADIUS;
        m_rectY[] = FRACTAL_RADIUS;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        int r = rand()%;
        outX = (x + m_rectX[r])*0.5f;
        outY = (y + m_rectY[r])*0.5f;
        outZ = z;
    }

    bool IsValidParamA() const {return true;}
    bool IsValidParamB() const {return true;}

    void SetParamA(float v)
    {
        m_ParamA = v;

        m_rectX[] = FRACTAL_RADIUS*m_ParamA;
        m_rectX[] = FRACTAL_RADIUS*m_ParamA;
        m_rectX[] = -FRACTAL_RADIUS*m_ParamA;
        m_rectX[] = -FRACTAL_RADIUS*m_ParamA;
    }

    void SetParamB(float v)
    {
        m_ParamB = v;

        m_rectY[] = FRACTAL_RADIUS*m_ParamB;
        m_rectY[] = -FRACTAL_RADIUS*m_ParamB;
        m_rectY[] = -FRACTAL_RADIUS*m_ParamB;
        m_rectY[] = FRACTAL_RADIUS*m_ParamB;
    }

private:
    float m_rectX[];
    float m_rectY[];
};

图形如下：

噢，SHIT，毫无规律可言。

那就变动一下吧：

class FractalSquare : public FractalEquation
{
public:
    FractalSquare()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_rectX[] = FRACTAL_RADIUS;
        m_rectY[] = FRACTAL_RADIUS;

        m_rectX[] = FRACTAL_RADIUS;
        m_rectY[] = -FRACTAL_RADIUS;

        m_rectX[] = -FRACTAL_RADIUS;
        m_rectY[] = -FRACTAL_RADIUS;

        m_rectX[] = -FRACTAL_RADIUS;
        m_rectY[] = FRACTAL_RADIUS;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        int r = rand()%;
        if (r < )
        {
            outX = (x + m_rectX[r])*0.5f;
            outY = (y + m_rectY[r])*0.5f;
        }
        else
        {
            outX = x*0.5f;
            outY = y*0.5f;
        }
        outZ = z;
    }

private:
    float m_rectX[];
    float m_rectY[];
};

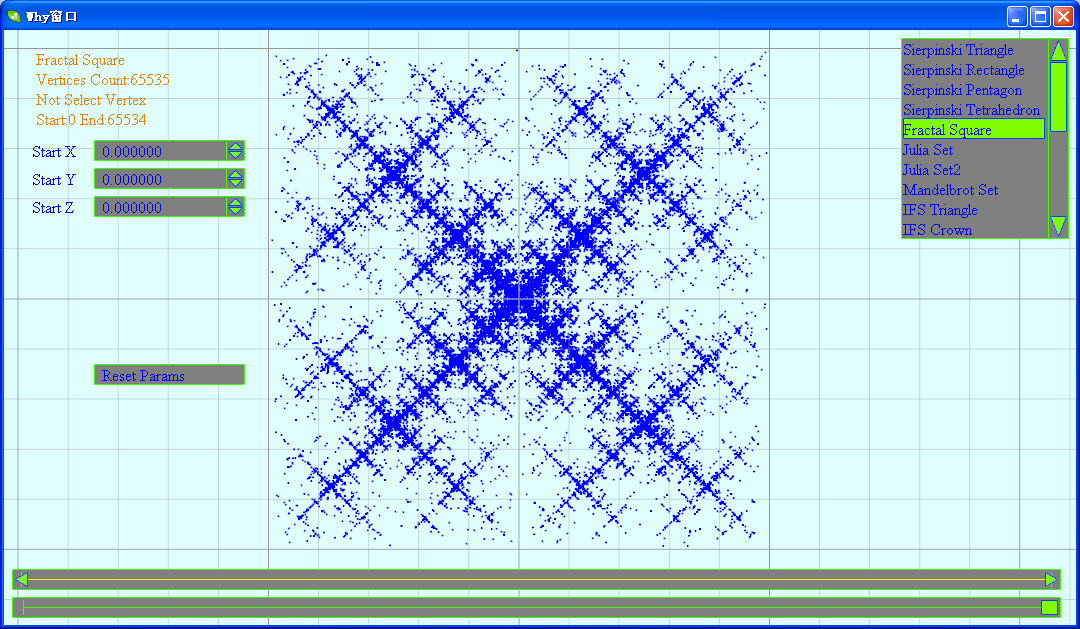
看上去还有点样。

（3）谢尔宾斯基五边形

四边形是不行的，那再试下五边：

// 五边形
class SierpinskiPentagon : public FractalEquation
{
public:
    SierpinskiPentagon()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        for (int i = ; i < ; i++)
        {
            m_pentagonX[i] = sinf(i*PI*/);
            m_pentagonY[i] = cosf(i*PI*/);
        }
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        int r = rand()%;
        outX = (x + m_pentagonX[r])*0.5f;
        outY = (y + m_pentagonY[r])*0.5f;
        outZ = z;
    }

private:
    float m_pentagonX[];
    float m_pentagonY[];
};

有点样子，那就以此算法为基础，生成幅图像看看：

有人称谢尔宾斯基三角形为谢尔宾斯基坟垛，当我看到这幅图时，有一种恐怖的感觉。邪恶的五角形，总感觉里面有数不清的骷髅。

看来二维空间中谢尔宾斯基的单数可以生成分形图形，而双数则为无序的混沌。

（4）谢尔宾斯基四面体

再由二维扩展到三维看看：

class SierpinskiTetrahedron : public FractalEquation
{
public:
    SierpinskiTetrahedron()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_vTetrahedron[] = YsVector(0.0f, 0.0f, 0.0f);
        m_vTetrahedron[] = YsVector(0.0f, 1.0f, 0.0f);
        m_vTetrahedron[] = YsVector(YD_REAL_SQRT_3/, 0.5f, 0.0f);
        m_vTetrahedron[] = YsVector(YD_REAL_SQRT_3/, 0.5f, YD_REAL_SQRT_3*YD_REAL_SQRT_2/);

        YsVector vCenter = m_vTetrahedron[] + m_vTetrahedron[] + m_vTetrahedron[] + m_vTetrahedron[];
        vCenter *= 0.25f;

        m_vTetrahedron[] -= vCenter;
        m_vTetrahedron[] -= vCenter;
        m_vTetrahedron[] -= vCenter;
        m_vTetrahedron[] -= vCenter;

        m_vTetrahedron[] *= FRACTAL_RADIUS;
        m_vTetrahedron[] *= FRACTAL_RADIUS;
        m_vTetrahedron[] *= FRACTAL_RADIUS;
        m_vTetrahedron[] *= FRACTAL_RADIUS;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        int r = rand()%;
        outX = (x + m_vTetrahedron[r].x)*0.5f;
        outY = (y + m_vTetrahedron[r].y)*0.5f;
        outZ = (z + m_vTetrahedron[r].z)*0.5f;
    }

    bool Is3D() const {return true;}

private:
    YsVector m_vTetrahedron[];
};

（5）其他

谢尔宾斯基三角形是一种很神的东西，我写过一些生成图像的算法，常常不知不觉中就出现了谢尔宾斯基三角形。如细胞生长机

再如：

之前我写过几篇与谢尔宾斯基分形相关的文章

分形之谢尔宾斯基(Sierpinski)三角形

分形之谢尔宾斯基(Sierpinski)地毯

分形之谢尔宾斯基(Sierpinski)四面体