最小生成树的两种方法（Kruskal算法和Prim算法）

关于图的几个概念定义：

• 连通图：在无向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该无向图为连通图。
• 强连通图：在有向图中，若任意两个顶点vivi与vjvj都有路径相通，则称该有向图为强连通图。
• 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
• 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
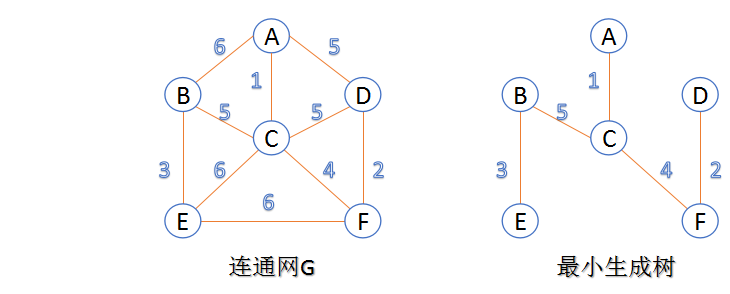
• 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

下面介绍两种求最小生成树算法

1.Kruskal算法

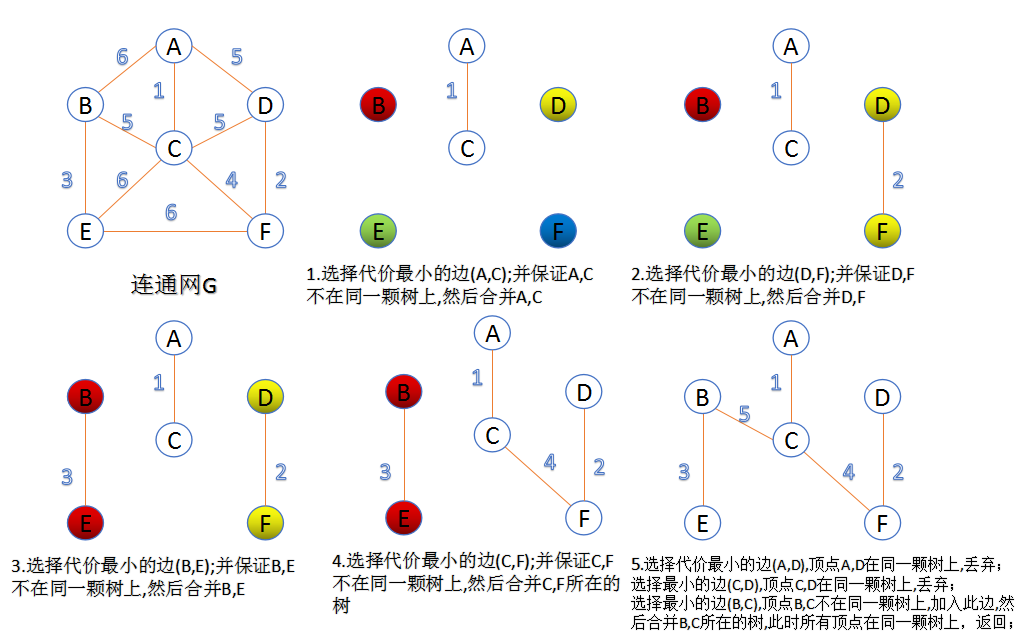
此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

1. 把图中的所有边按代价从小到大排序；
2. 把图中的n个顶点看成独立的n棵树组成的森林；
3. 按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

2. Prim算法

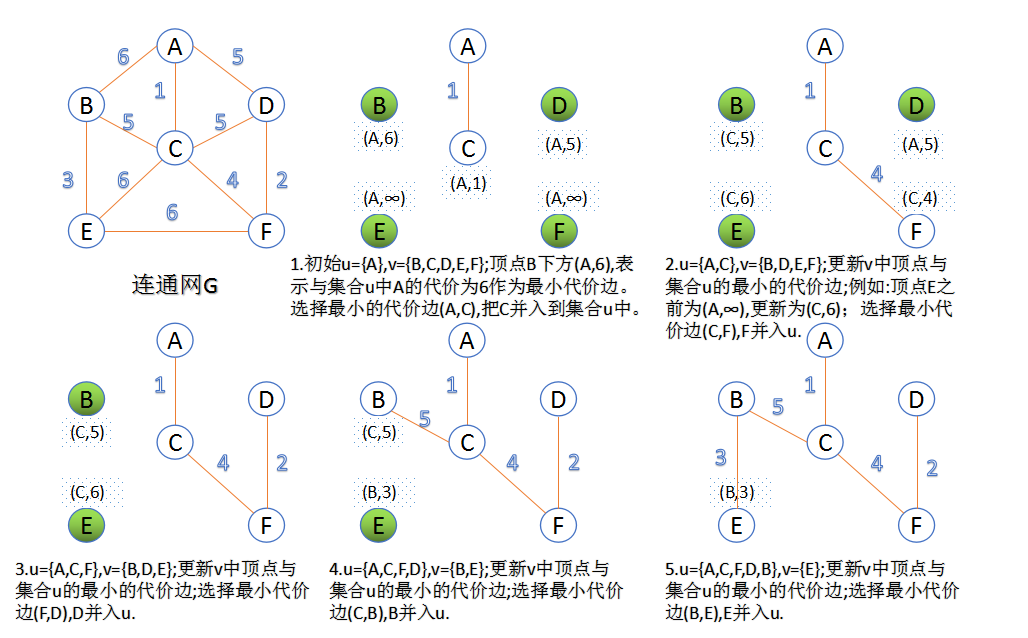
此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

1. 图的所有顶点集合为VV；初始令集合u={s},v=V−uu={s},v=V−u;
2. 在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u0,v0)(u0,v0)，加入到最小生成树中，并把v0v0并入到集合u中。
3. 重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

由于不断向集合u中加点，所以最小代价边必须同步更新；需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息，：

struct
{
  char vertexData   //表示u中顶点信息
  UINT lowestcost   //最小代价
}closedge[vexCounts]

3. 完整代码

/************************************************************************
CSDN 勿在浮沙筑高台 http://blog.csdn.net/luoshixian099算法导论--最小生成树（Prim、Kruskal）2016年7月14日
************************************************************************/
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define INFINITE 0xFFFFFFFF
#define VertexData unsigned int  //顶点数据
#define UINT  unsigned int
#define vexCounts 6  //顶点数量
char vextex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };
struct node
{
    VertexData data;
    unsigned int lowestcost;
}closedge[vexCounts]; //Prim算法中的辅助信息
typedef struct
{
    VertexData u;
    VertexData v;
    unsigned int cost;  //边的代价
}Arc;  //原始图的边信息
void AdjMatrix(unsigned int adjMat[][vexCounts])  //邻接矩阵表示法
{
    for (int i = 0; i < vexCounts; i++)   //初始化邻接矩阵
        for (int j = 0; j < vexCounts; j++)
        {
            adjMat[i][j] = INFINITE;
        }
    adjMat[0][1] = 6; adjMat[0][2] = 1; adjMat[0][3] = 5;
    adjMat[1][0] = 6; adjMat[1][2] = 5; adjMat[1][4] = 3;
    adjMat[2][0] = 1; adjMat[2][1] = 5; adjMat[2][3] = 5; adjMat[2][4] = 6; adjMat[2][5] = 4;
    adjMat[3][0] = 5; adjMat[3][2] = 5; adjMat[3][5] = 2;
    adjMat[4][1] = 3; adjMat[4][2] = 6; adjMat[4][5] = 6;
    adjMat[5][2] = 4; adjMat[5][3] = 2; adjMat[5][4] = 6;
}
int Minmum(struct node * closedge)  //返回最小代价边
{
    unsigned int min = INFINITE;
    int index = -1;
    for (int i = 0; i < vexCounts;i++)
    {
        if (closedge[i].lowestcost < min && closedge[i].lowestcost !=0)
        {
            min = closedge[i].lowestcost;
            index = i;
        }
    }
    return index;
}
void MiniSpanTree_Prim(unsigned int adjMat[][vexCounts], VertexData s)
{
    for (int i = 0; i < vexCounts;i++)
    {
        closedge[i].lowestcost = INFINITE;
    }
    closedge[s].data = s;      //从顶点s开始
    closedge[s].lowestcost = 0;
    for (int i = 0; i < vexCounts;i++)  //初始化辅助数组
    {
        if (i != s)
        {
            closedge[i].data = s;
            closedge[i].lowestcost = adjMat[s][i];
        }
    }
    for (int e = 1; e <= vexCounts -1; e++)  //n-1条边时退出
    {
        int k = Minmum(closedge);  //选择最小代价边
        cout << vextex[closedge[k].data] << "--" << vextex[k] << endl;//加入到最小生成树
        closedge[k].lowestcost = 0; //代价置为0
        for (int i = 0; i < vexCounts;i++)  //更新v中顶点最小代价边信息
        {
            if ( adjMat[k][i] < closedge[i].lowestcost)
            {
                closedge[i].data = k;
                closedge[i].lowestcost = adjMat[k][i];
            }
        }
    }
}
void ReadArc(unsigned int  adjMat[][vexCounts],vector<Arc> &vertexArc) //保存图的边代价信息
{
    Arc * temp = NULL;
    for (unsigned int i = 0; i < vexCounts;i++)
    {
        for (unsigned int j = 0; j < i; j++)
        {
            if (adjMat[i][j]!=INFINITE)
            {
                temp = new Arc;
                temp->u = i;
                temp->v = j;
                temp->cost = adjMat[i][j];
                vertexArc.push_back(*temp);
            }
        }
    }
}
bool compare(Arc  A, Arc  B)
{
    return A.cost < B.cost ? true : false;
}
bool FindTree(VertexData u, VertexData v,vector<vector<VertexData> > &Tree)
{
    unsigned int index_u = INFINITE;
    unsigned int index_v = INFINITE;
    for (unsigned int i = 0; i < Tree.size();i++)  //检查u,v分别属于哪颗树
    {
        if (find(Tree[i].begin(), Tree[i].end(), u) != Tree[i].end())
            index_u = i;
        if (find(Tree[i].begin(), Tree[i].end(), v) != Tree[i].end())
            index_v = i;
    }

    if (index_u != index_v)   //u,v不在一颗树上，合并两颗树
    {
        for (unsigned int i = 0; i < Tree[index_v].size();i++)
        {
            Tree[index_u].push_back(Tree[index_v][i]);
        }
        Tree[index_v].clear();
        return true;
    }
    return false;
}
void MiniSpanTree_Kruskal(unsigned int adjMat[][vexCounts])
{
    vector<Arc> vertexArc;
    ReadArc(adjMat, vertexArc);//读取边信息
    sort(vertexArc.begin(), vertexArc.end(), compare);//边按从小到大排序
    vector<vector<VertexData> > Tree(vexCounts); //6棵独立树
    for (unsigned int i = 0; i < vexCounts; i++)
    {
        Tree[i].push_back(i);  //初始化6棵独立树的信息
    }
    for (unsigned int i = 0; i < vertexArc.size(); i++)//依次从小到大取最小代价边
    {
        VertexData u = vertexArc[i].u;
        VertexData v = vertexArc[i].v;
        if (FindTree(u, v, Tree))//检查此边的两个顶点是否在一颗树内
        {
            cout << vextex[u] << "---" << vextex[v] << endl;//把此边加入到最小生成树中
        }
    }
}

int main()
{
    unsigned int  adjMat[vexCounts][vexCounts] = { 0 };
    AdjMatrix(adjMat);   //邻接矩阵
    cout << "Prim :" << endl;
    MiniSpanTree_Prim(adjMat,0); //Prim算法，从顶点0开始.
    cout << "-------------" << endl << "Kruskal:" << endl;
    MiniSpanTree_Kruskal(adjMat);//Kruskal算法
    return 0;
}