hdoj-1233-还是畅通工程

题目：hdoj-1233

题解：

本题是典型的最小生成树问题，给出的是无向图，这里使用的方法是Prim最小生成树算法。

Reference

Prim算法参照：最小生成树-Prim算法和Kruskal算法，讲的很详细了。

测试的时候可以参考这幅图：

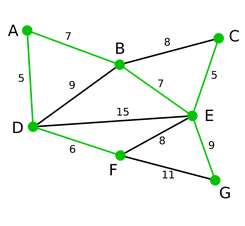
算法介绍：

主要步骤(摘自上文链接)：

1).输入：一个加权连通图，其中顶点集合为V，边集合为E；

2).初始化：Vnew = {x}，其中x为集合V中的任一节点（起始点），Enew = {},为空；

3).重复下列操作，直到Vnew = V：

a.在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

b.将v加入集合Vnew中，将<u, v>边加入集合Enew中；

4).输出：使用集合Vnew和Enew来描述所得到的最小生成树。

本题维护两个数组：

(1)Primgh二维数组，存储图。

(2)refer数组，判断一个节点是否在Vnew中。

用于存边的数组Enew在本题中不需要。

代码：

//
//  main.cpp
//  Prim_1233
//
//  Created by wasdns on 16/11/24.
//  Copyright © 2016年 wasdns. All rights reserved.
//
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <string>
#include <string.h>
#define maxn 10000005;
using namespace std;
int Primgh[10000][10000];                        //存储图
bool refer[10005];                               //判断是否在Enew中
/*
    用于初始化的函数
 */
void Initial(int n, int m)
{
    int i, j;
    for (i = 1; i <= n; i++)
    {
        refer[i] = false;
        for (j = 1; j <= n; j++)
        {
            if (i == j) {
                Primgh[i][j] = 0;
            }
            else Primgh[i][j] = maxn;
        }
    }
    int u, v, w;
    for (i = 1; i <= m; i++)
    {
        cin >> u >> v >> w;
        Primgh[u][v] = w;
        Primgh[v][u] = w;
    }
}
/*
    Prim算法，主体部分
 */
int Prim_Alg(int n, int m)
{
    Initial(n, m);
    int i, j, k;
    int ans = 0;
    //最小生成树的路径长度                 
    refer[1] = true;
    //选择点1出发        
    //最小生成树一共有n-1条边，因此需要寻找最短边n-1次，基于贪心
    for (i = 1; i <= n-1; i++)
    {
        int minlen = maxn;
        //minlen: 在Vnew中的节点所连接的边中，寻找cost最小的边
        int rcd = 1;
        //cost最小的边有两个节点，rcd记录其中的不属于Vnew的节点
        for (j = 1; j <= n; j++)
        {
            if (!refer[j]) continue;
            //遍历Vnew中的所有节点
            int len1 = maxn;
            //对于Vnew中的某个节点来说，所连接的最短的路径cost大小
            int rcd1 = 1;
            //对于Vnew中的某个节点来说，rcd记录的节点
            //贪心，寻找这个节点连接的cost最小的路径
            for (k = 1; k <= n; k++)
            {
                if (!refer[k])
                {
                    if (Primgh[j][k] < len1) {
                        len1 = Primgh[j][k];
                        rcd1 = k;
                    }
                }
            }
            if (len1 < minlen) {
                //判断贪心得到的路径是否是全局cost最短
                minlen = len1;
                rcd = rcd1;
            }
        }
        /*Debug：*/
        //char check = 'A'+rcd-1;
        //cout << "rcd: " << check << endl;
        //cout << "minlen: " << minlen << endl;
        refer[rcd] = true;
        //贪心求出cost最小的路径，rcd记录的节点入Vnew
        rcd = 1;
        //重置rcd
        ans += minlen;
    }
    return ans;
}
int main()
{
    int n, m;
    while (scanf("%d", &n) != EOF)
    {
        if (n == 0) break;
        m = n * (n-1) / 2;
        cout << Prim_Alg(n, m) << endl;
    }
    return 0;
}

2016/11/24