VAE论文学习

intractable棘手的，难处理的  posterior distributions后验分布 directed probabilistic有向概率

approximate inference近似推理  multivariate Gaussian多元高斯  diagonal对角 maximum likelihood极大似然

参考：https://blog.csdn.net/yao52119471/article/details/84893634

VAE论文所在讲的问题是：

我们现在就是想要训练一个模型P(x),并求出其参数Θ：

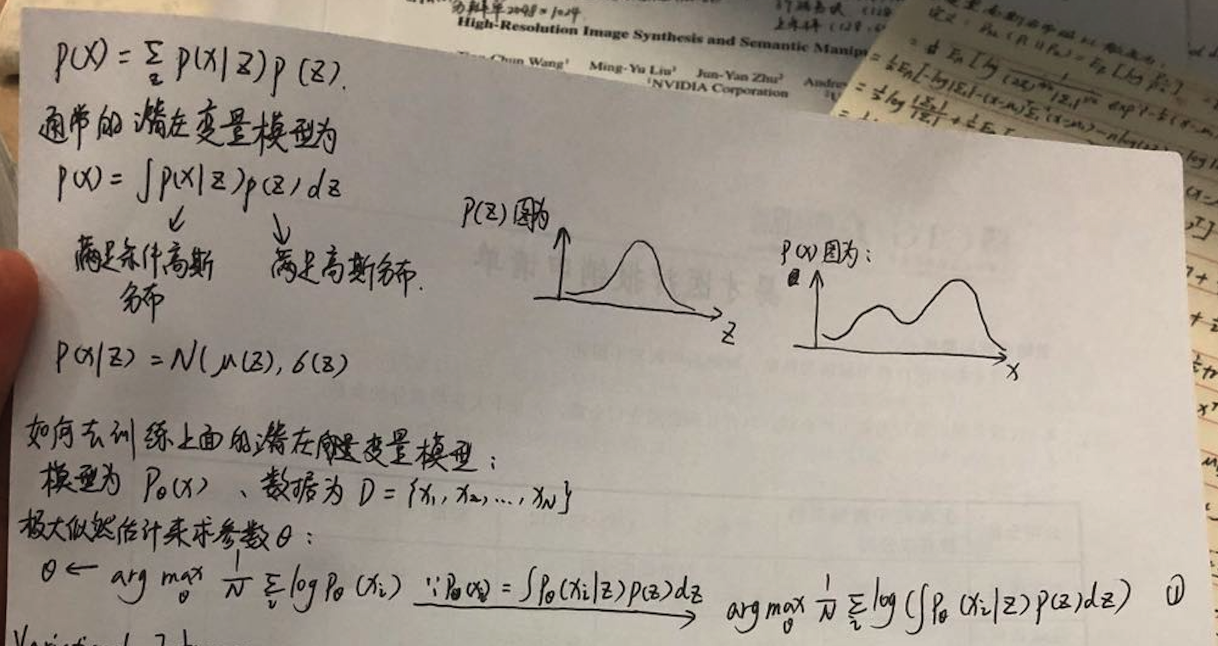
通过极大似然估计求其参数

Variational Inference

在论文中P(x)模型会被拆分成两部分，一部分由数据x生成潜在向量z，即p_θ(z|X)；一部分从z重新在重构数据x，即p_θ(X|z)

实现过程则是希望能够使用一个q_Φ(z|X)模型去近似p_θ(z|X)，然后作为模型的Encoder；后半部分p_θ(X|z)则作为Decoder，Φ/θ表示参数，实现一种同时学习识别模型参数φ和参数θ的生成模型的方法，推导过程为：

现在问题就在于怎么进行求导，因为现在模型已经不是一个完整的P(x) = p_θ(z|X) + p_θ(X|z),现在变成了P(x) = q_Φ(z|X) + p_θ(X|z),那么如果对Φ求导就会变成一个问题，因此论文中就提出了一个reparameterization trick方法：

取样于一个标准正态分布来采样z，以此将q_Φ(z|X) 和p_θ(X|z)两个子模型通过z连接在了一起

最终的目标函数为：

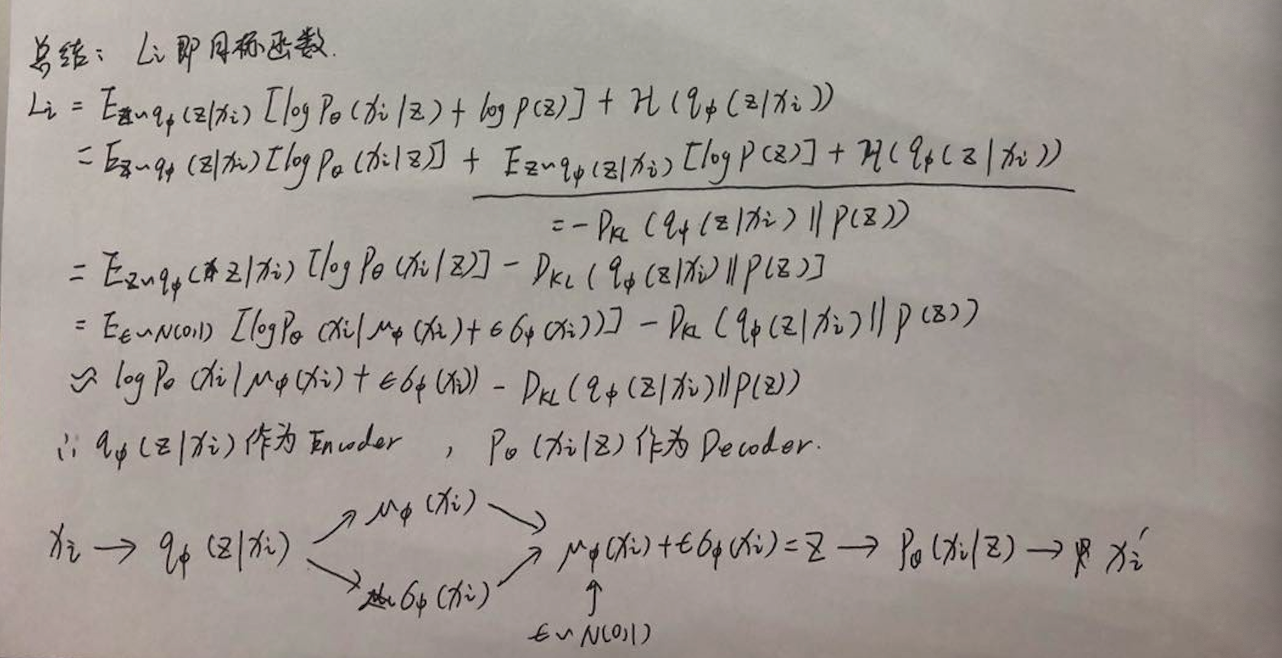
因此目标函数 = 输入和输出x求MSELoss - KL(q_Φ(z|X) || p_θ(z))

在论文上对式子最后的KL散度 -KL(q_Φ(z|X) || p_θ(z))的计算有简化为：

多维KL散度的推导可见：KL散度

假设p_θ(z)服从标准正态分布，采样ε服从标准正态分布满足该假设

简单代码实现：

import torch
from torch.autograd import Variable
import numpy as np
import torch.nn.functional as F
import torchvision
from torchvision import transforms
import torch.optim as optim
from torch import nn
import matplotlib.pyplot as plt
 
class Encoder(torch.nn.Module):
    def __init__(self, D_in, H, D_out):
        super(Encoder, self).__init__()
        self.linear1 = torch.nn.Linear(D_in, H)
        self.linear2 = torch.nn.Linear(H, D_out)
 
    def forward(self, x):
        x = F.relu(self.linear1(x))
        return F.relu(self.linear2(x))
 
class Decoder(torch.nn.Module):
    def __init__(self, D_in, H, D_out):
        super(Decoder, self).__init__()
        self.linear1 = torch.nn.Linear(D_in, H)
        self.linear2 = torch.nn.Linear(H, D_out)
 
    def forward(self, x):
        x = F.relu(self.linear1(x))
        return F.relu(self.linear2(x))
 
class VAE(torch.nn.Module):
    latent_dim = 
 
    def __init__(self, encoder, decoder):
        super(VAE, self).__init__()
        self.encoder = encoder
        self.decoder = decoder
        self._enc_mu = torch.nn.Linear(, )
        self._enc_log_sigma = torch.nn.Linear(, )
 
    def _sample_latent(self, h_enc):
        """
        Return the latent normal sample z ~ N(mu, sigma^)
        """
        mu = self._enc_mu(h_enc)
        log_sigma = self._enc_log_sigma(h_enc) #得到的值是loge(sigma)
        sigma = torch.exp(log_sigma) # = e^loge(sigma) = sigma
        #从均匀分布中取样
        std_z = torch.from_numpy(np.random.normal(, , size=sigma.size())).float()
 
        self.z_mean = mu
        self.z_sigma = sigma
 
        return mu + sigma * Variable(std_z, requires_grad=False)  # Reparameterization trick
 
    def forward(self, state):
        h_enc = self.encoder(state)
        z = self._sample_latent(h_enc)
        return self.decoder(z)
 
# 计算KL散度的公式
def latent_loss(z_mean, z_stddev):
    mean_sq = z_mean * z_mean
    stddev_sq = z_stddev * z_stddev
    return 0.5 * torch.mean(mean_sq + stddev_sq - torch.log(stddev_sq) - )
 
if __name__ == '__main__':
 
    input_dim =  *
    batch_size = 
 
    transform = transforms.Compose(
        [transforms.ToTensor()])
    mnist = torchvision.datasets.MNIST('./', download=True, transform=transform)
 
    dataloader = torch.utils.data.DataLoader(mnist, batch_size=batch_size,
                                             shuffle=True, num_workers=)
 
    print('Number of samples: ', len(mnist))
 
    encoder = Encoder(input_dim, , )
    decoder = Decoder(, , input_dim)
    vae = VAE(encoder, decoder)
 
    criterion = nn.MSELoss()
 
    optimizer = optim.Adam(vae.parameters(), lr=0.0001)
    l = None
    for epoch in range():
        for i, data in enumerate(dataloader, ):
            inputs, classes = data
            inputs, classes = Variable(inputs.resize_(batch_size, input_dim)), Variable(classes)
            optimizer.zero_grad()
            dec = vae(inputs)
            ll = latent_loss(vae.z_mean, vae.z_sigma)
            loss = criterion(dec, inputs) + ll
            loss.backward()
            optimizer.step()
            l = loss.data[]
        print(epoch, l)
 
    plt.imshow(vae(inputs).data[].numpy().reshape(, ), cmap='gray')
    plt.show(block=True)