P3374 【模板】树状数组 1（线段树）

【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 x

• 求出某区间每一个数的和

输入格式

第一行包含两个正整数 n,m ，分别表示该数列数字的个数和操作的总个数。

第二行包含 n 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 m 行每行包含 3 个整数，表示一个操作，具体如下：

• 1 x k 含义：将第 x 个数加上 k

• 2 x y 含义：输出区间 [x,y] 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

样例 #1

样例输入 #1

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

样例输出 #1

14
16

提示

【数据范围】

对于 30% 的数据，1 ≤ n ≤ 8，$1 ≤ m ≤ 10；

对于 70% 的数据，1 ≤ n,m ≤ 10^4；

对于 100% 的数据，1 ≤ n,m ≤ 5 * 10^5。

数据保证对于任意时刻，a 的任意子区间（包括长度为 1 和 n 的子区间）和均在 [-2^{31}, 2^{31}) 范围内。

样例说明：

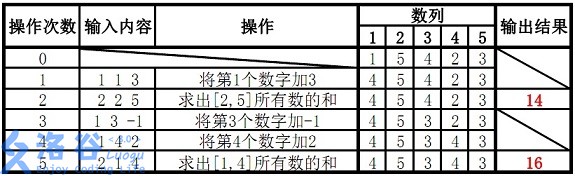
故输出结果14、16

思路：树状数组？线段树?

三步走!!!

1. 建树

   void buildtree(int k,int l,int r){
   	if(l==r){//l==r时就是分到只剩一个了
   		f[k]=a[l];//此时返回叶子结点数据（也就是原数据）
   		return;
   	}
   //以下三步，就是找左右儿子
   //这个过程与归并排序的递归过程类似可以去看一下
   //其中2k和2k+1代表的是当前结点的左右子结点（这一步不详细展开，可以自己画图尝试）
   	int mid=(l+r)>>1;
   	buildtree(2*k,l,mid);
   	buildtree(2*k+1,mid+1,r);
   
   //父亲结点=儿子结点的和
   	f[k]=f[2*k]+f[2*k+1];
   }
   

2. 修改数据

   void add(int k,int l,int r,int x,int y){//k表示第几个结点，l、r表示区间，x表示第几个值要修改，y表示要使原值+y
   	//因为每次找到的都是第x个元素的父亲结点的父亲的父亲……所以直接+y
   	f[k]+=y;//包含结点x的值都需要+y
   	if(l==r) return;当递归到l=r即为只有一个元素返回
   	int mid=(l+r)>>1;
   	if(x<=mid) add(2*k,l,mid,x,y);如果是在左子树就往左找
   	else add(2*k+1,mid+1,r,x,y);如果是在右子树就往右边找
   
   }
   

3. 计算答案

   int calc(int k,int l,int r,int s,int t){//s、t表示要求的区间反围
   	if(l==s && r==t)//如果区间缩小到包含原数据区间的子区间反围即返回
   		return f[k];
   	int mid=(l+r)>>1;
   	if(t<=mid)
   		return calc(2*k,l,mid,s,t);//如果当前要求的区间范围在左子树就往左边找
   	else//在右子树或者部分在右子树
   		if(s>mid)
   			return calc(2*k+1,mid+1,r,s,t);//在右子树上
   		else
   			return calc(2*k,l,mid,s,mid)+calc(2*k+1,mid+1,r,mid+1,t);//部分在右子树
   }
   

tips：这个树状数组应该开多大?

开4n。参考证明连接：线段树需要开4倍区间大小的数组的原因_线段树数组一般开 n*4 的大小-CSDN博客

（本文章仅供学习交流如有侵权请私信立刻删除）

AC Code

// Problem:
//     P3374 【模板】树状数组 1
//
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3374
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include<iostream>
#include<algorithm>
//#include<cstdio>

#define ll long long
#define endl '\n'
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>(b);i--)
#define N 2000100 //1e6+100
#define M 500010
using namespace std;
int f[N],a[M],n,m;
void buildtree(int k,int l,int r){
	if(l==r){
		f[k]=a[l];
		return;
	}
	int mid=(l+r)>>1;
	buildtree(2*k,l,mid);
	buildtree(2*k+1,mid+1,r);
	f[k]=f[2*k]+f[2*k+1];
}
void add(int k,int l,int r,int x,int y){
	f[k]+=y;
	if(l==r) return;
	int mid=(l+r)>>1;
	if(x<=mid) add(2*k,l,mid,x,y);
	else add(2*k+1,mid+1,r,x,y);
}
int calc(int k,int l,int r,int s,int t){
	if(l==s && r==t)
		return f[k];
	int mid=(l+r)>>1;
	if(t<=mid)
		return calc(2*k,l,mid,s,t);
	else
		if(s>mid)
			return calc(2*k+1,mid+1,r,s,t);
		else
			return calc(2*k,l,mid,s,mid)+calc(2*k+1,mid+1,r,mid+1,t);
}
int main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	rep(i,1,n)
		cin>>a[i];
	buildtree(1,1,n);
	int t,x,y;
	while(m--){
		cin>>t>>x>>y;
		if(t==1)
			add(1,1,n,x,y);
		else cout<<calc(1,1,n,x,y)<<endl;;
	}
	return 0;
}