poj 2446 Chessboard (二分图利用奇偶性匹配)

Chessboard

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 13176		Accepted: 4118

Description

Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the
figure below). 




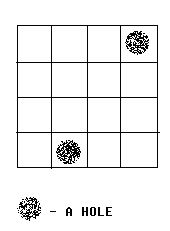
We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below: 

1. Any normal grid should be covered with exactly one card. 

2. One card should cover exactly 2 normal adjacent grids. 



Some examples are given in the figures below: 

 

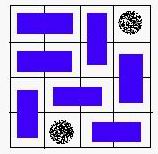
A VALID solution.


 

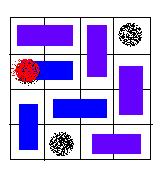
An invalid solution, because the hole of red color is covered with a card.


 

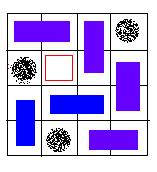
An invalid solution, because there exists a grid, which is not covered.


Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

Input

There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and holes. In the next k lines, there is a pair of integers (x, y) in each line, which represents a hole in the y-th row, the x-th column.

Output

If the board can be covered, output "YES". Otherwise, output "NO".

Sample Input

4 3 2
2 1
3 3

Sample Output

YES

Hint

 

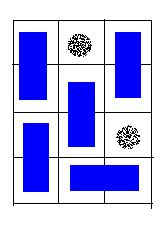
A possible solution for the sample input.

给你一个棋盘，棋盘上有几个洞。要求你用一些1*2的卡片覆盖没有洞的区域，一个格子仅仅能有一张卡片覆盖。

看能否恰好覆盖。





二分匹配：利用二分匹配。两个能匹配的格子的坐标和必定奇偶性不同。利用这一点能够降低时间耗费。

#include"stdio.h"
#include"string.h"
#include"queue"
using namespace std;
#define N 35
#define M 1200
int g[N][N],n,m;
int dir[4][2]={0,1,0,-1,-1,0,1,0};
int mark[M],link[M];
int judge(int x,int y)
{
    if(x>=0&&x<n&&y>=0&&y<m)
        return 1;
    return 0;
}
int find(int k)
{
    int i,j,x,y,di,dj;
    x=k/m;
    y=k%m;
    for(i=0;i<4;i++)
    {
        di=dir[i][0]+x;
        dj=dir[i][1]+y;
        if(judge(di,dj)&&!g[di][dj])
        {
            j=di*m+dj;
            if(!mark[j])
            {
                mark[j]=1;
                if(link[j]==-1||find(link[j]))
                {
                    link[j]=k;
                    return 1;
                }
            }
        }
    }
    return 0;
}
int main()
{
    int u,v,k,i,j;
    while(scanf("%d%d%d",&n,&m,&k)!=-1)
    {
        memset(g,0,sizeof(g));
        for(i=0;i<k;i++)
        {
            scanf("%d%d",&v,&u);
            u--;v--;
            g[u][v]=1;
        }
        if((n*m-k)&1)
        {
            printf("NO\n");
            continue;
        }
        int ans=0;
        memset(link,-1,sizeof(link));
        for(i=0;i<n;i++)
        {
            for(j=0;j<m;j++)
            {
                if((i+j)%2==0||g[i][j])      //(i+j)奇偶性！

！！
                    continue;
                memset(mark,0,sizeof(mark));
                ans+=find(i*m+j);
            }
        }
        //printf("%d\n",ans);
        if(ans*2==n*m-k)
            printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}