【转】LCS

　　动态规划法

　　经常会遇到复杂问题不能简单地分解成几个子问题，而会分解出一系列的子问题。简单地采用把大问题分解成子问题，并综合子问题的解导出大问题的解的方法，问题求解耗时会按问题规模呈幂级数增加。

　　为了节约重复求相同子问题的时间，引入一个数组，不管它们是否对最终解有用，把所有子问题的解存于该数组中，这就是动态规划法所采用的基本方法。

　　【问题】 求两字符序列的最长公共字符子序列

　　问题描述：字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。令给定的字符序列X=“x0，x1，…，xm-1”，序列Y=“y0，y1，…，yk-1”是X的子序列，存在X的一个严格递增下标序列<i0，i1，…，ik-1>，使得对所有的j=0，1，…，k-1，有xij=yj。例如，X=“ABCBDAB”，Y=“BCDB”是X的一个子序列。

　　考虑最长公共子序列问题如何分解成子问题，设A=“a0，a1，…，am-1”，B=“b0，b1，…，bm-1”，并Z=“z0，z1，…，zk-1”为它们的最长公共子序列。不难证明有以下性质：

　　（1） 如果am-1=bn-1，则zk-1=am-1=bn-1，且“z0，z1，…，zk-2”是“a0，a1，…，am-2”和“b0，b1，…，bn-2”的一个最长公共子序列；

　　（2） 如果am-1!=bn-1，则若zk-1!=am-1，蕴涵“z0，z1，…，zk-1”是“a0，a1，…，am-2”和“b0，b1，…，bn-1”的一个最长公共子序列；

　　（3） 如果am-1!=bn-1，则若zk-1!=bn-1，蕴涵“z0，z1，…，zk-1”是“a0，a1，…，am-1”和“b0，b1，…，bn-2”的一个最长公共子序列。

　　这样，在找A和B的公共子序列时，如有am-1=bn-1，则进一步解决一个子问题，找“a0，a1，…，am-2”和“b0，b1，…，bm-2”的一个最长公共子序列；如果am-1!=bn-1，则要解决两个子问题，找出“a0，a1，…，am-2”和“b0，b1，…，bn-1”的一个最长公共子序列和找出“a0，a1，…，am-1”和“b0，b1，…，bn-2”的一个最长公共子序列，再取两者中较长者作为A和B的最长公共子序列。

　　求解：

　　引进一个二维数组c[][]，用c[i][j]记录X[i]与Y[j] 的LCS 的长度，b[i][j]记录c[i][j]是通过哪一个子问题的值求得的，以决定搜索的方向。
　　我们是自底向上进行递推计算，那么在计算c[i,j]之前，c[i-1][j-1]，c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j]，就可以计算出c[i][j]。

　　问题的递归式写成：

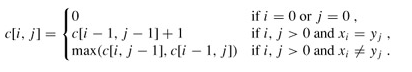
　　回溯输出最长公共子序列过程：

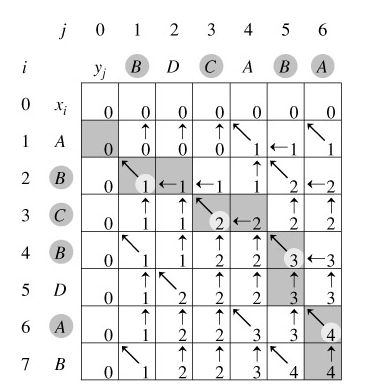
　　算法分析：
　　由于每次调用至少向上或向左（或向上向左同时）移动一步，故最多调用(m + n)次就会遇到i = 0或j = 0的情况，此时开始返回。返回时与递归调用时方向相反，步数相同，故算法时间复杂度为Θ(m + n)。

　　代码：

#include <stdio.h>
#include <string.h>
#define MAXLEN 100
//x 字符串a
//y 字符串b
//m 字符串a的长度
//n 字符串b的长度
//c x[i]、y[i]对应的lcs的长度
//b 确定打印时的搜寻方向。是向上走还是向左走
void LCSLength(char *x, char *y, int m, int n, int c[][MAXLEN], int b[][MAXLEN])
{
    int i, j;

    for(i = ; i <= m; i++)
        c[i][] = ;
    for(j = ; j <= n; j++)
        c[][j] = ;
    for(i = ; i<= m; i++)
    {
        for(j = ; j <= n; j++)
        {
            if(x[i-] == y[j-])
            {
                c[i][j] = c[i-][j-] + ;
                b[i][j] = ;
            }
            else if(c[i-][j] >= c[i][j-])
            {
                c[i][j] = c[i-][j];
                b[i][j] = ;
            }
            else
            {
                c[i][j] = c[i][j-];
                b[i][j] = -;
            }
        }
    }
}

void PrintLCS(int b[][MAXLEN], char *x, int i, int j)
{
    if(i ==  || j == )
        return;
    if(b[i][j] == )
    {
        PrintLCS(b, x, i-, j-);
        printf("%c ", x[i-]);
    }
    else if(b[i][j] == )
        PrintLCS(b, x, i-, j);
    else
        PrintLCS(b, x, i, j-);
}

int main(int argc, char **argv)
{
    char x[MAXLEN] = {"ABCBDAB"};//字符串a
    char y[MAXLEN] = {"BDCABA"};//字符串b
    int b[MAXLEN][MAXLEN];//
    int c[MAXLEN][MAXLEN];//a[i]、b[j]对应的lcs长度
    int m, n;

    m = strlen(x);//字符串a的长度
    n = strlen(y);//字符串b的长度

    LCSLength(x, y, m, n, c, b);
    PrintLCS(b, x, m, n);

    return ;
}

转自http://blog.csdn.net/yysdsyl/article/details/4226630