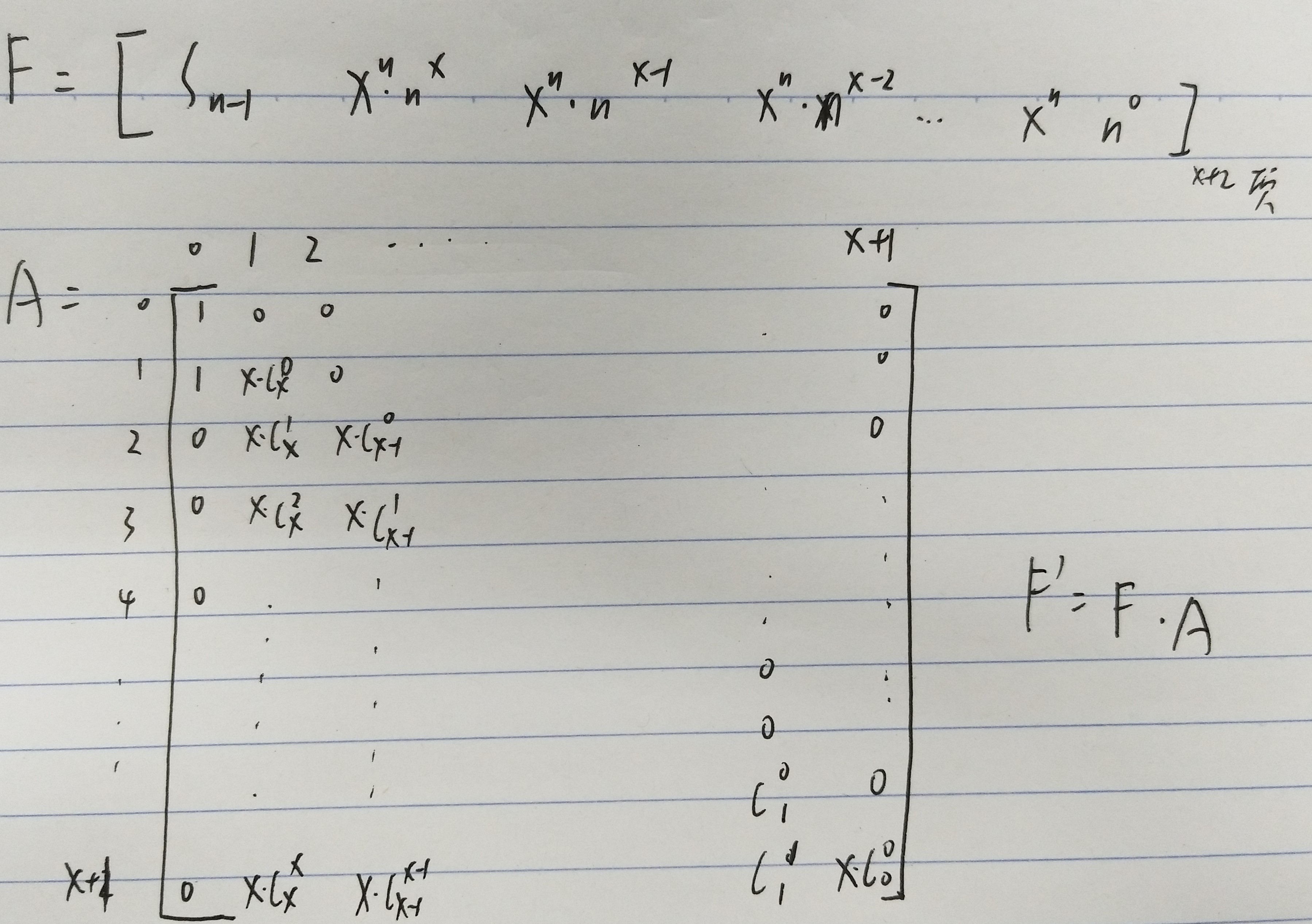hdu3483 A Very Simple Problem 非线性递推方程2 矩阵快速幂
题目描述:给出n,x,mod。求s[n].
s[n]=s[n-1]+(x^n)*(n^x)%mod;
思路:这道题是hdu5950的进阶版。大家可以看这篇博客hdu5950题解。
由于n很大,所以肯定是矩阵快速幂的题目,但是矩阵快速幂只能解决线性的问题,n^4在这个式子中是非线性的,后一项和前一项没有什么直接关系,这里要做一个转换,把n^4变成一个线性的,也就是和(n-1)^4有关系的东西,而这个办法就是:
n^4=(n-1+1)^4=(n-1)^4+4*(n-1)^3+6*(n-1)^2+4*(n-1)^1+(n-1)^0;
而x^n是一个线性的东西,只需要在构造A矩阵的时候在矩阵中多乘以一个x就可以了。
但这道题卡住我的地方是,里面需要算组合数,我之前算组合数的方法是用逆元来求,但是逆元只能处理mod为质数的情况,而这道题mod不是质数,所以不可以这样做(题目还算良心,样例给出的就是合数,否则估计wa死),而要用
c[i][j]=c[i-1][j-1]+c[i-1][j]%mod, 来递推,也就是这样。
inline void init() {
cc[0][0]=cc[1][0]=cc[1][1]=1;
for(int i=2;i<=50;i++){
cc[i][0]=cc[i][i]=1;
for(int j=1;j<i;j++){
cc[i][j]=cc[i-1][j]+cc[i-1][j-1]%mod;
}
}
}而这个矩阵是怎样的呢
完整代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<string.h>
#include<sstream>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<stack>
#include<bitset>
#define CLR(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f3f;
inline int rd(void) {
int x=0;int f=1;
char s=getchar();
while(s<'0'||s>'9') { if(s=='-')f=-1; s=getchar();}
while(s>='0'&&s<='9') { x=x*10+s-'0'; s=getchar();}
x*=f;return x;}
ll n,x,mod;
ll cc[55][55];
inline void init() {
cc[0][0]=cc[1][0]=cc[1][1]=1;
for(int i=2; i<=50; i++) {
cc[i][0]=cc[i][i]=1;
for(int j=1; j<i; j++) {
cc[i][j]=cc[i-1][j]+cc[i-1][j-1]%mod;
}
}
}
ll f[55],a[55][55];
void mul(ll f[55],ll a[55][55],ll n) {
ll c[55];
CLR(c,0);
for(int j=0; j<n; j++) {
for(int k=0; k<n; k++) {
c[j]=(c[j]+f[k]*a[k][j]%mod)%mod;
}
}
memcpy(f,c,sizeof(c));
}
void mulself(ll a[55][55],ll n) {
ll c[55][55];
CLR(c,0);
for(int i=0; i<n; i++) {
for(int j=0; j<n; j++) {
for(int k=0; k<n; k++) {
c[i][j]=(c[i][j]+a[i][k]*a[k][j]%mod)%mod;
}
}
}
memcpy(a,c,sizeof(c));
}
int main() {
while(scanf("%lld%lld%lld",&n,&x,&mod)) {
if(n==-1)break;
if(n==1) {
printf("%lld\n",x);
} else {
init();
CLR(f,0),CLR(a,0);
f[0]=x;
for(int i=1; i<=x+1; i++) {
f[i]=((ll)pow(2,x-i+1))%mod*x%mod*x%mod;
}
a[0][0]=1,a[1][0]=1;
for(int j=1; j<=x+1; j++) {
for(int i=j; i<=x+1; i++) {
a[i][j]=x*cc[x+1-j][i-j]%mod;
}
}
n--;
for(; n; n>>=1) {
if(n&1)mul(f,a,x+2);
mulself(a,x+2);
}
printf("%lld\n",f[0]);
}
}
}A Very Simple Problem
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 1244 Accepted Submission(s): 608
Problem Description
This is a very simple problem. Given three integers N, x, and M, your task is to calculate out the following value:
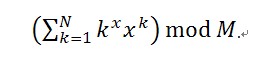
Input
There are several test cases. For each case, there is a line with three integers N, x, and M, where 1 ≤ N, M ≤ 2*109, and 1 ≤ x ≤ 50.
The input ends up with three negative numbers, which should not be processed as a case.
Output
For each test case, print a line with an integer indicating the result.
Sample Input
100 1 10000 3 4 1000 -1 -1 -1
Sample Output
5050 444
hdu3483 A Very Simple Problem 非线性递推方程2 矩阵快速幂的更多相关文章
- 【66测试20161115】【树】【DP_LIS】【SPFA】【同余最短路】【递推】【矩阵快速幂】
还有3天,今天考试又崩了.状态还没有调整过来... 第一题:小L的二叉树 勤奋又善于思考的小L接触了信息学竞赛,开始的学习十分顺利.但是,小L对数据结构的掌握实在十分渣渣.所以,小L当时卡在了二叉树. ...
- Luogu3824 [NOI2017]泳池 【多项式取模】【递推】【矩阵快速幂】
题目分析: 用数论分块的思想,就会发现其实就是连续一段的长度$i$的高度不能超过$\lfloor \frac{k}{i} \rfloor$,然后我们会发现最长的非$0$一段不会超过$k$,所以我们可以 ...
- HDU4565 So Easy! —— 共轭构造、二阶递推数列、矩阵快速幂
题目链接:https://vjudge.net/problem/HDU-4565 So Easy! Time Limit: 2000/1000 MS (Java/Others) Memory L ...
- ACM学习历程—SNNUOJ 1116 A Simple Problem(递推 && 逆元 && 组合数学 && 快速幂)(2015陕西省大学生程序设计竞赛K题)
Description Assuming a finite – radius “ball” which is on an N dimension is cut with a “knife” of N- ...
- UVA10655 Contemplation! Algebra —— 推公式、矩阵快速幂
题目链接:https://vjudge.net/problem/UVA-10655 题意: a+b.ab的值分别为p.q,求a^n+b^n. 题解: 1.a.b未知,且直接求出a.b也不太实际. 2. ...
- hdu 2604 Queuing(推推推公式+矩阵快速幂)
Description Queues and Priority Queues are data structures which are known to most computer scientis ...
- HDU 5950 - Recursive sequence - [矩阵快速幂加速递推][2016ACM/ICPC亚洲区沈阳站 Problem C]
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5950 Farmer John likes to play mathematics games with ...
- A Simple Math Problem (矩阵快速幂)
Lele now is thinking about a simple function f(x). If x < 10 f(x) = x. If x >= 10 f(x) = a0 ...
- HDU-6185-Covering(推递推式+矩阵快速幂)
Covering Time Limit: 5000/2500 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Su ...
随机推荐
- touch: cannot touch `/home/tomcat7/logs/catalina.out': Permission denied
今天打开虚拟机启动tomcat,Y的包这个错,普通用户登录的,一直报这个错误,竟然没有想起来是为什么,真是感到惭愧,其实原因很简单,就是logs文件夹没有读写的权限,一条 chmod -R 777 l ...
- hibernate的子查询
hibernate原话 HQL supports subqueries in the where clause. We can't think of many good uses for subque ...
- WPA密码攻击宝典
原则:密码以8-10位为主.11位仅限于当地手机号.一般人的多年用数字做密码的习惯和心理,先数 字.再字母,或数字.字母重复几遍,字符几乎全用小写,所以淘汰大写及"~!@#$%^&* ...
- oracle create user &tablespace & imp
一.表空间 1.创建表空间 CREATE TABLESPACE 空间名称 DATAFILE '文件名1' SIZE 数字M [,'文件名2' SIZE 数字….] EXTENT MANAGEMENT ...
- 【总结整理】WebGIS学习-thinkGIS(三):关于影像金字塔、瓦片行列号、分辨率resolution
http://www.thinkgis.cn/topic/541a5206da8db186fd0673ba 1.前言 在上一节中我们知道了屏幕上一像素等于实际中多少单位长度(米或经纬度)的换算方法,而 ...
- cocos2d中setBlendFunc设置颜色混合方案
CCSprite有一个ccBlendFunc类型的blendFunc_结构体成员,可以用来设置描绘时的颜色混合方案.ccBlendFunc包含了一个src和一个dst,分别表示源和目标的运算因子. 如 ...
- JAVA语法规则总结
单继承多实现 抽象类 抽象方法 使用关键字:abstract修饰的方法就是抽象方法; 抽象方法的形式:只有方法的声明,没有方法体; 抽象方法一般存在于父类中,相当于强制要求子类必须重写该方法,相当于 ...
- opencv新版本的数据结构
转自 http://blog.csdn.net/yang_xian521/article/details/7108387 记得我在OpenCV学习笔记(四)——新版本的数据结构core里面讲过新版本的 ...
- git clone Timed out 解决
因为不可抗拒的原因,在乌鲁木齐从 github 上面克隆项目时,会超时克隆不了. 使用 https 方式报错: $ git clone https://github.com/xxx.git Cloni ...
- Entity Framework Tutorial Basics(15):Querying with EDM
Querying with EDM: We have created EDM, DbContext, and entity classes in the previous sections. Here ...