[题解]图的m着色问题

图的m着色问题(color)

[题目描述]

给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。如果有一种着色法使G中每条边的2个顶点着不同颜色，则称这个图是m可着色的。图的m着色问题是对于给定图G和m种颜色，找出所有不同的着色法。

[编程任务]

对于给定的无向连通图G和m种不同的颜色，编程计算图的所有不同的着色法。

[输入格式]

第1行有3个正整数n，k 和m，表示给定的图G有n个顶点和k条边，m种颜色。顶点编号为1，2，…，n。接下来的k行中，每行有2个正整数u,v，表示图G 的一条边(u,v)。

[输出格式]

将计算出的不同的着色方案数输出。

[输入样例]

5 8 4

1 2

1 3

1 4

2 3

2 4

2 5

3 4

4 5

[输出样例]

48

[解法]

此题大致思路是DFS每次确定一个点的颜色，直到确定图所有点的颜色。还有就是要会存图，通常用tu[x][y]来表示两点之间的关系，tu[x][y]=-1表示x、y两点无连接；非-1表示两点的权值或距离。我的代码中应题做了一些改变：用tu[x][y] 来表示两点之间的关系和颜色，tu[x][y]=-1表示x、y两点无连接；tu[x][y]=0表示y点没有确定颜色；tu[x][y]=k表示y点颜色为k。有了这些写代码就变得异常的简单，只需注意几个细节。

细节1：

初始化：初始值为-1，表示所有点都没有连接。

点的连接为双向的！点的连接为双向的！点的连接为双向的！

并且此时x、y都是没有确定颜色的。

细节2：

回溯时要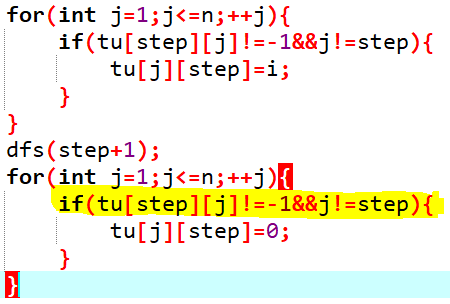注意只回溯与step有连接的点！

否则回导致所有点对step都有联系

还有一定要吧step点本身排除不然会没有解，

因为不管什么时候step点的颜色都与step点的颜色一样

[代码(AC)]

 #include <iostream>
 #include <cstdio>
 #include <cmath>
 #include <string>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 int tu[][];
 int n,k,m;
 long long ans=;
 void dfs(int step){
     if(step>n){
         ++ans;
         return ;
     }
     for(int i=;i<=m;++i){//试探每种颜色
         bool flag=true;
         for(int j=;j<=n;++j){
             if(tu[step][j]!=-&&i==tu[step][j]){
                 flag=false;
                 break;
             }
         }
         if(flag){
             for(int j=;j<=n;++j){
                 if(tu[step][j]!=-&&j!=step){
                     tu[j][step]=i;
                 }
             }
             dfs(step+);
             for(int j=;j<=n;++j){
                 if(tu[step][j]!=-&&j!=step){
                     tu[j][step]=;
                 }
             }
         }
     }
 }
 int main(){
     freopen("color.in","r",stdin);
     freopen("color.out","w",stdout);
     memset(tu,-,sizeof(tu));
     scanf("%d%d%d",&n,&k,&m);
     for(int i=;i<k;++i){
         int x,y;
         scanf("%d%d",&x,&y);
         tu[x][y]=;
         tu[y][x]=;
     }
     dfs();
     printf("%d",ans);
     return ;
 }

2018-10-06 13:16:17