poj 1423 打表/斯特林公式

对于n位数的计算，我们可以采用(int)log10(n) + 1的方法得到n的位数

第一种方法：

对于n！位数的计算，log10(n!) = log10(1) + log10(2) + ... + log10(n)

为防止直接暴力超时这部分运算可以打表等待主程序调用

#include<iostream>
#include<cmath>
using namespace std;

const int MAXN = 1e7;
int ans[MAXN +];

void action(int m)//打表计算n!位数，存在ans数组中
{
    double d = ;
    for(int i = ;i<=m;i++)
    {
        d += log10(double(i));//累加log10(i)
        ans[i] = (int)d + ;//向下取整并+1
    }
}

int main()
{
    int n,m;
    cin>>n;
    action(MAXN);
    while(n--)
    {
        cin>>m;
        cout<<ans[m]<<endl;
    }
    return ;
}

第二种方法：

对于n!的计算，也可以用斯特林公式：

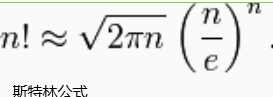
然后直接计算(int)log10(n!) + 1

#include<iostream>
#include<cmath>
using namespace std;

double pi = acos((double)-);

int main()
{
    int n,m;
    cin>>n;
    while(n--)
    {
        cin>>m;
        cout<<(int)(log10(sqrt( * m * pi) )+ m * log10(m / exp((double))))+ <<endl;
    }
}