【learning】二分图最大匹配的König定理

　[吐槽]

　　嗯好吧这个东西吧。。其实是一开始做一道最小点覆盖的题的时候学到的奇妙深刻的东西

　　然后发现写了很长

　　然后就觉得不拎出来对不起自己呀哈哈哈哈

　　咳咳好的进入正题

[正题]

　　在这里码一下最小点覆盖的相关知识

　　http://www.matrix67.com/blog/archives/116 （二分图最大匹配的König定理及其证明）

　　（所以说其实我也很想知道为什么那个o上面有两个点啊哈哈哈哈）

　　

　　嗯还是把自己对于上面那篇东西的理解写一下吧整理整理qwq

　　König定理

　　一个二分图中最大的匹配数=该图中最小点覆盖数

　　嗯首先还是先把定义搬出来吧

　　点覆盖：就是一个点集，满足该图的所有边都有至少一个顶点在这个点集中，点集大小最小的成为最小点覆盖

　　

　　证明的话稍微整理一下（learn from matrix67%%%）

　　假设我们现在已经跑出了一个最大匹配，匹配数为$m$，考虑构造一种点覆盖的可行方案

　　 一个简单的想法：

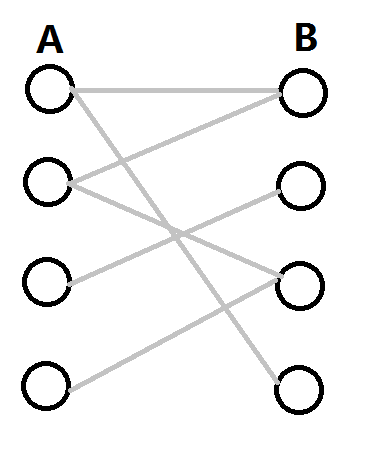
　　我们按照一种方式给这堆点打上标记，以B部分中所有没有被匹配到的点为起点，顺着匈牙利算法中的交错轨（也就是匹配边和非匹配边交替着走）遍历直到不能走下去了为止，并给沿路上的点全部打上标记

　　现在我们将B部分中没有打上标记的点和A部分中打上标记的点变成一个点集

　　这个点集就是一种可行的点覆盖，而且是最小点覆盖

　　为啥？

　　我们先将交错轨标号所有的一些奇妙性质列出来再进行证明会比较方便一点

　　对于一条在交错轨上的边$(u,v)$，必定满足：

　　1.$u，v$均为标号点

　　2.若该边为匹配边，则遍历时先走到$u$再走到$v$，即从A部分到B部分

　　3.若改变为非匹配边，则遍历时先走到$v$再走到$u$，即从B部分走到A部分

　　首先，证明一下这是一个点覆盖

　　我们可以把边分为两类，一类是在某条交错轨上的边，一类不在

　　对于在交错轨上面的边，显然我可以通过选取A部分中打上标记也就是遍历到的点来覆盖掉

　　而对于不在交错轨上且没有被覆盖到的边，它在B部分的端点一定是没有被标记的

　　（否则就说明其在A部分的端点一定是没有被标记的，

　　而这种边是不可能存在的，用反证法

　　设存在一条边$(u,v)$，$u$没被标记，$v$被标记，

　　则$v$应该被交错轨经过

　　若这条边是匹配边，则一定是由$u$走到$v$，也就是说$v$的标记一定来自$u$，

　　因此$u$也应该有标记，矛盾

　　若这条边是非匹配边，则到$v$的交错轨可以继续走下去

　　这条边也应该在交错轨上，矛盾

　　综上，不存在这种边）

　　所以这种选法就一定可以保证所有的边都被覆盖到啦

　　第二，证明一下这个点覆盖的大小$=m$

　　首先看我们选的用来覆盖交错轨上的边的点

　　因为我们在标记的时候走的是一段段的交错轨，并且我们的起点是在右边

　　所以左边的A部分中被标记的点的个数必定与交错轨中匹配边的个数相等

　　接着看剩下的部分

　　由于交错轨标号方式，交错轨上的边的两端的点必定都是被标记的点

　　换句话来说就是非交错轨上的且没有被覆盖到的边的右端点肯定连到的是未被标记的B部分的点

　　而每个未被标记的B部分的点必定会连且只会连出一条匹配边（继续反证嗯，比较简单不写了）

　　所以数量也是相同的　　
　　

　　所以两个加一下就是$m$啦

　　最后，证明这是最小点覆盖

　　嗯。。一句话搞定：覆盖$m$条匹配边最少都要$m$个点，所以当然就是最小的啦

　　搞掂捞面ovo