bzoj3672【NOI2014】购票

题目描述

 　　今年夏天，NOI在SZ市迎来了她30周岁的生日。来自全国 n 个城市的OIer们都会从各地出发，到SZ市参加这次盛会。

       全国的城市构成了一棵以SZ市为根的有根树，每个城市与它的父亲用道路连接。为了方便起见，我们将全国的 n 个城市用 1 到 n 的整数编号。其中SZ市的编号为 1。对于除SZ市之外的任意一个城市 v，我们给出了它在这棵树上的父亲城市 fv  以及到父亲城市道路的长度 sv。

从城市 v 前往SZ市的方法为：选择城市 v 的一个祖先 a，支付购票的费用，乘坐交通工具到达 a。再选择城市 a 的一个祖先 b，支付费用并到达 b。以此类推，直至到达SZ市。

对于任意一个城市 v，我们会给出一个交通工具的距离限制 lv。对于城市 v 的祖先 a，只有当它们之间所有道路的总长度不超过 lv 时，从城市 v 才可以通过一次购票到达城市 a，否则不能通过一次购票到达。对于每个城市 v，我们还会给出两个非负整数 pv,qv 作为票价参数。若城市 v 到城市 a 所有道路的总长度为 d，那么从城市 v 到城市 a 购买的票价为 dpv+qv。

　　每个城市的OIer都希望自己到达SZ市时，用于购票的总资金最少。你的任务就是，告诉每个城市的OIer他们所花的最少资金是多少。

---

输入格式

　　第 1 行包含2个非负整数 n,t，分别表示城市的个数和数据类型（其意义将在后面提到）。输入文件的第 2 到 n 行，每行描述一个除SZ之外的城市。其中第 v 行包含 5 个非负整数 $f_v,s_v,p_v,q_v,l_v$，分别表示城市 v 的父亲城市，它到父亲城市道路的长度，票价的两个参数和距离限制。请注意：输入不包含编号为 1 的SZ市，第 2 行到第 n 行分别描述的是城市 2 到城市 n。

---

输出格式

　　输出包含 n-1 行，每行包含一个整数。其中第 v 行表示从城市 v+1 出发，到达SZ市最少的购票费用。同样请注意：输出不包含编号为 1 的SZ市。

---

数据规模

---

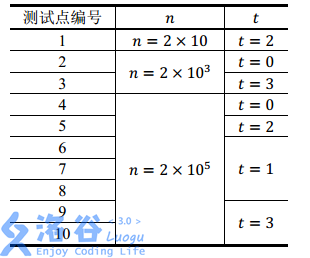
• 题解：

  • 设$v$是$u$的祖先，$dp[u] = dp[v] + (dis[u]-dis[v])*p[u] + q[u] \  , \  (dis[u]-dis[v]<=l[u])$
  • 斜率优化部分：
  • 假设$d[v_{1}]<d[v_{2}]$且对$u$来说$v2$比$v1$更优：
  • $$dp[v_{1}]+(dis[u]-dis[v_{1}])*p[u]+q[u] > dp[v_{2}]+(dis[u]-dis[v_{2}])*p[u]+q[u] ;$$
  • $$\frac{dp[v_{2}]-dp[v_{1}]}{dis[v2]-dis[v1]} < p[u]$$
  • 可以维护$(dis[v],dp[v])$的下凸包(斜率单调上升)；
  • 由于是在一颗树上且有$l$的限制，所以我们需要用用一些方法维护一下，
  • 可以找树的重心分治，我写的树剖：
  • 对每个重链的顶端维护一个凸包，$dfs$的时候不断加入点；
  • 我们先$dfs$轻儿子，这样一个点到根的轻链的父亲都是一个凸包的末端；
  • 找转移点的时候不断向上跳，如果某条链全部满足限制则在重链顶端的凸包上直接查询；
  • 否则一定是合法的分界点在当前找到的链上，用线段树维护区间的凸包查询即可；
  • 一次最多找到$log$条树链，最多有一条树链需要在线段树里面查询；
  • 算上三分，时间复杂度：$O(nlog^2n)$
  • 有个小技巧，线段树满了之后再做凸包

 #include<bits/stdc++.h>
 #define ls (k<<1)
 #define rs (k<<1|1)
 #define ll long long
 #define ld double
 using namespace std;
 const int N=;
 char gc(){
     static char*p1,*p2,s[];
     if(p1==p2)p2=(p1=s)+fread(s,,,stdin);
     return(p1==p2)?EOF:*p1++;
 }
 ll rd(){
     ll x=; char c=gc();
     while(c<''||c>'')c=gc();
     while(c>=''&&c<='')x=(x<<)+(x<<)+c-'',c=gc();
     return x;
 }
 int n,T,f[N],o=,hd[N],dep[N],fa[N][],bin[];
 int idx,sz[N],tp[N],sn[N],mx[N],id[N],cnt[N<<],st[N];
 ll dp[N],tmp,dis[N],s[N],p[N],q[N],l[N];
 struct Poi{
     ld x,y;
     Poi(ld _x=,ld _y=):x(_x),y(_y){};
     Poi operator -(const Poi&a){return Poi(x-a.x,y-a.y);}
     ld operator ^(const Poi&a){return x*a.y-y*a.x;}
     bool operator <(const Poi&a){return x==a.x?y<a.y:x<a.x;}
 }P[N];
 vector<int>g1[N<<],g2[N];
 struct Edge{int v,nt;}E[N];
 void adde(int u,int v){E[o]=(Edge){v,hd[u]};hd[u]=o++;}
 void dfs1(int u){
     sz[u]=;
     fa[u][]=f[u];
     dep[u]=dep[f[u]]+;
     dis[u]=dis[f[u]]+s[u];
     for(int i=;bin[i]<dep[u];++i)fa[u][i]=fa[fa[u][i-]][i-];
     for(int i=hd[u];i;i=E[i].nt){
         int v=E[i].v;
         dfs1(v);
         sz[u]+=sz[v];
         if(sz[v]>sz[sn[u]])sn[u]=v;
     }
 }
 void dfs2(int u,int t){
     tp[u]=t;
     id[u]=++idx;
     st[idx]=u;
     if(sn[u])dfs2(sn[u],t);
     for(int i=hd[u];i;i=E[i].nt){
         int v=E[i].v;
         if(v==sn[u])continue;
         dfs2(v,v);
     }
 }
 inline bool judge(int a,int b,int c){return ((P[b]-P[a])^(P[c]-P[b]))<=;}
 void pushup(int k){
     int l=ls,r=rs,tl=,tr=;
     while(tl<(int)g1[l].size()||tr<(int)g1[r].size()){
         if(tr==(int)g1[r].size()||(tl<(int)g1[l].size()&&g1[l][tl]<g1[r][tr])){
             while(g1[k].size()>&&judge(g1[k][g1[k].size()-],g1[k].back(),g1[l][tl]))g1[k].pop_back();
             g1[k].push_back(g1[l][tl++]);
         }else{
             while(g1[k].size()>&&judge(g1[k][g1[k].size()-],g1[k].back(),g1[r][tr]))g1[k].pop_back();
             g1[k].push_back(g1[r][tr++]);
         }
     }
 }
 void ins1(int k,int l,int r,int u){
     cnt[k]++;
     if(l==r){g1[k].push_back(u);return;}
     int mid=(l+r)>>;
     if(id[u]<=mid)ins1(ls,l,mid,u);
     else ins1(rs,mid+,r,u);
     if(tp[st[l]]==tp[st[r]]&&cnt[k]==r-l+)pushup(k);
 }
 void ins2(int k,int u){
     while(g2[k].size()>&&judge(g2[k][g2[k].size()-],g2[k].back(),u))g2[k].pop_back();
     g2[k].push_back(u);
 }
 inline bool ok(int u,int v){return dis[u]-dis[v]<=l[u];}
 inline void upd(ll&x,ll y){if(x>y)x=y;}
 void cal(vector<int>&g,int u){
     int l=,r=g.size()-;
     while(r-l>){
         int mid=(r-l)/,mid1=l+mid,mid2=r-mid;
         ll t1=dp[g[mid1]]-dis[g[mid1]]*p[u];
         ll t2=dp[g[mid2]]-dis[g[mid2]]*p[u];
         if(t1>t2)l=mid1+;
         else r=mid2-;
     }
     for(int i=l;i<=r;++i)upd(tmp,dp[g[i]]-dis[g[i]]*p[u]);
 }
 void query1(int k,int l,int r,int x,int y,int u){
     if(l==x&&r==y){cal(g1[k],u);return;}
     int mid=(l+r)>>;
     if(y<=mid)query1(ls,l,mid,x,y,u);
     else if(x>mid)query1(rs,mid+,r,x,y,u);
     else query1(ls,l,mid,x,mid,u),query1(rs,mid+,r,mid+,y,u);
 }
 void query2(int x,int u){
     cal(g2[x],u);
 }
 void solve(int u){
     tmp=u==?:9e18;
     for(int x=f[u],t=tp[x];x;x=f[t],t=tp[x]){
         if(dep[mx[u]]<dep[t])query2(id[t],u);
         else {query1(,,n,id[mx[u]],id[x],u);break;}
     }
     dp[u]=dis[u]*p[u]+q[u]+tmp;
     P[u]=Poi(dis[u],dp[u]);
     ins1(,,n,u);
     ins2(id[tp[u]],u);
 }
 void calmx(int u){
     int t=u;
     for(int i=;~i;--i)if(fa[t][i]&&ok(u,fa[t][i]))t=fa[t][i];
     mx[u]=t;
 }
 void dfs3(int u){
     calmx(u);
     solve(u);
     for(int i=hd[u];i;i=E[i].nt){
         int v=E[i].v;
         if(v==sn[u])continue;
         dfs3(v);
     }
     if(sn[u])dfs3(sn[u]);
 }
 int main(){
     #ifndef ONLINE_JUDGE
     freopen("bzoj3672.in","r",stdin);
     freopen("bzoj3672.out","w",stdout);
     #endif
     for(int i=bin[]=;i<=;++i)bin[i]=bin[i-]<<;
     n=rd();T=rd();
     for(int i=;i<=n;++i){
         adde(f[i]=rd(),i);
         s[i]=rd();p[i]=rd();
         q[i]=rd();l[i]=rd();
     }
     dfs1();
     dfs2(,);
     dfs3();
     for(int i=;i<=n;++i)printf("%lld\n",dp[i]);
     return ;
 }