[洛谷P2750] [USACO5.5]贰五语言Two Five

洛谷题目链接:[USACO5.5]贰五语言Two Five

题目描述

有一种奇怪的语言叫做“贰五语言”。它的每个单词都由A～Y这25个字母各一个组成。但是，并不是任何一种排列都是一个合法的贰五语言单词。贰五语言的单词必须满足这样一个条件：把它的25个字母排成一个5*5的矩阵，它的每一行和每一列都必须是递增的。比如单词ACEPTBDHQUFJMRWGKNSXILOVY，它排成的矩阵如下所示：

A C E P T

B D H Q U

F J M R W

G K N S X

I L O V Y

因为它的每行每列都是递增的，所以它是一个合法的单词。而单词YXWVUTSRQPONMLKJIHGFEDCBA则显然不合法。 由于单词太长存储不便，需要给每一个单词编一个码。编码方法如下：从左到右，再从上到下，可以由一个矩阵的得到一个单词，再把单词按照字典顺序排序。比如，单词ABCDEFGHIJKLMNOPQRSTUVWXY的编码为1，而单词ABCDEFGHIJKLMNOPQRSUTVWXY的编码为2。

现在，你需要编一个程序，完成单词与编码间的转换。

输入输出格式

输入格式：

第一行为一个字母N或W。N表示把编码转换为单词，W表示把单词转换为编码。

若第一行为N，则第二行为一个整数，表示单词的编码。若第一行为W，则第二行为一个合法的单词。

输出格式：

每行一个整数或单词。

输入输出样例

输入样例#1：

N

2

输出样例#1：

ABCDEFGHIJKLMNOPQRSUTVWXY

输入样例#2：

W

ABCDEFGHIJKLMNOPQRSUTVWXY

输出样例#2：

2

说明

题目翻译来自NOCOW。

USACO Training Section 5.5

题解: 我尝试过爆搜,但是在我\(A\)了这题之后都还没枚举完所有情况...

显然这个状态是非常多的,接近\(25!\),所以我们需要将其中一些状态记忆化一下.

我们设\(f[a][b][c][d][e]\)表示第\(1\)行填入了\(a\)个数,第\(2\)行填入了\(b\)个数....的方案.因为我们在填数的时候一定是一个像这样的形状(转自zyzzyzzyzzyz的图):

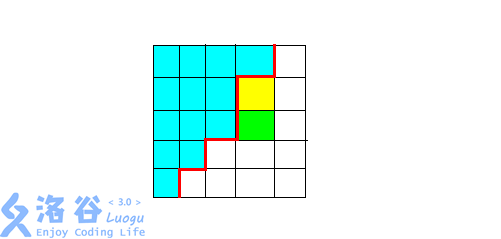
要填入绿色的块之前一定要先填入黄色的块.

那么我们可以计算出方案数之后,就考虑如何计算答案.我们可以通过类似倍增求\(lca\)的方式来统计答案.回忆一下倍增是如何求\(lca\)的?从大到小枚举向上跳的距离,如果超过了就不跳.这里也是类似的方法.

我们在求方案数的时候会用一个\(vis\)数组来记录某个数字是否可以用,那么在我们修改限制的时候,每次计算出的方案数很显然是会不一样的,这时候就可以用我们上面提到的方法了.

具体细节有点讲不太清,看代码吧.

#include<bits/stdc++.h>
using namespace std;

int n, vis[30];
int f[7][7][7][7][7];
char opt, s[30];

bool ok(int x, int num){
    return !vis[x] || vis[x] == num;
}

int dfs(int a, int b, int c, int d, int e, int x){
    if(x == 26) return 1;
    if(f[a][b][c][d][e]) return f[a][b][c][d][e];
    int res = 0;
    if(a <= 5 && ok(a, x)) res += dfs(a+1, b, c, d, e, x+1);
    if(b < a && ok(b+5, x)) res += dfs(a, b+1, c, d, e, x+1);
    if(c < b && ok(c+10, x)) res += dfs(a, b, c+1, d, e, x+1);
    if(d < c && ok(d+15, x)) res += dfs(a, b, c, d+1, e, x+1);
    if(e < d && ok(e+20, x)) res += dfs(a, b, c, d, e+1, x+1);
    return f[a][b][c][d][e] = res;
}

int main(){
    int tmp; cin >> opt;
    if(opt == 'N'){
        cin >> n;
        for(int i = 1; i <= 25; i++){
            for(vis[i] = 1; ; vis[i]++){
                memset(f, 0, sizeof(f));
                tmp = dfs(1, 1, 1, 1, 1, 1);
                if(tmp >= n) break;
                n -= tmp;
            }
        }
        for(int i = 1; i <= 25; i++) cout << (char)(vis[i]-1+'A');
        cout << endl;
    }
    else {
        int res = 0; cin >> s+1;
        for(int i = 1; i <= 25; i++)
            for(vis[i] = 1; vis[i] < s[i]-'A'+1; vis[i]++){
                memset(f, 0, sizeof(f));
                res += dfs(1, 1, 1, 1, 1, 1);
            }
        cout << res+1 << endl;
    }
    return 0;
}