快速求popcount的和

前置知识

\(\text{popcount}(n)\) 表示将 \(n\) 转为二进制后的数中 \(1\) 的个数。

结论

\[\sum_{i=1}^{n} \text{ popcount}(i)=\sum_{i=1}^{\left \lceil \log_{2}{n} \right \rceil-1 } \left [ (n>>(i-1))\text{&}1==1 \right ] \times (i\times 2^{i-1}+2^{i}\times \text {popcount}(n>>i)
\]

其中 $ \left [ (n>>(i-1))\text{&}1==1 \right ]$ 表示 \(n\) 转成二进制以后第 \(i\) 位是不是 \(0\)。

原理

首先我们需要知道这个东西：

__builtin_popcount(x)

可恶怎么又是 STL

他的作用就是求出 \(x\) 的 \(\text{popcount}\) 值，这个东西好像很快我们先把他当作 \(O(1)\) 的。

接下来我们考虑用 \(O(1)\) 的时间来求得

\[\sum_{i=0}^{2^{k}-1} \text{popcount}(i)
\]

的做法。

这里以 $ \left [ 0,2^{5}-1 \right ] $ 为例。

先把所有的数都给列出来。

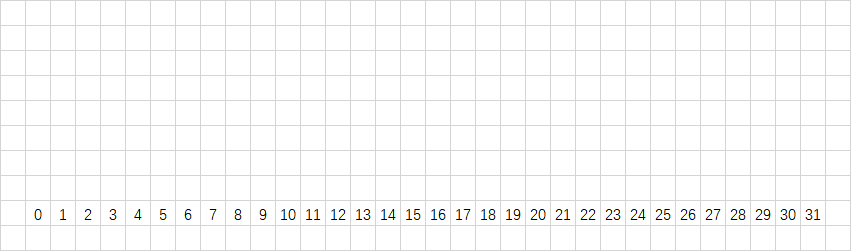
然后我们可以看到最低位的规律。

依次向后走。

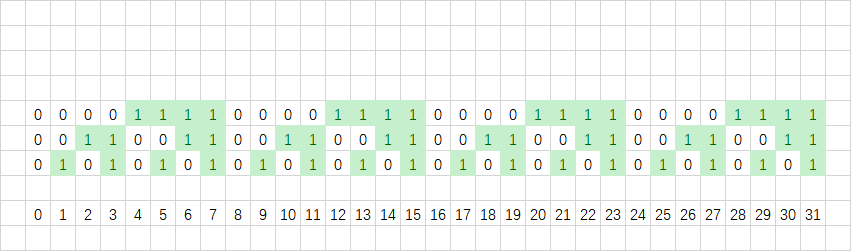
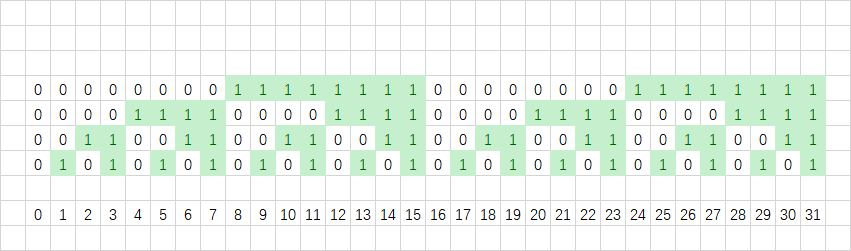
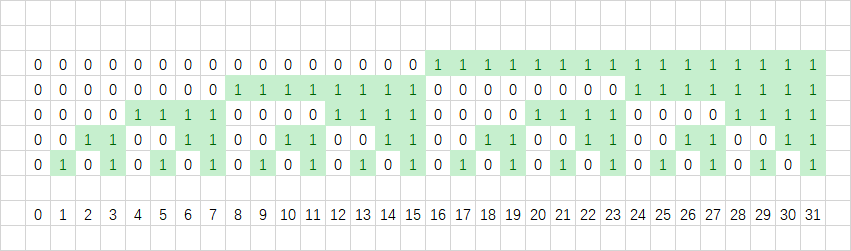
我们可以看到每一位里面都是一半是 \(0\)，一半是 \(1\)。

因此我们可以得到下面的公式：

\[\sum_{i=0}^{2^{k}-1} \text{popcount}(i)=k\times 2^{k-1}
\]

下面以 \((11010110)_{2}=(214)_{10}\) 为例。

其第一位为 \(1\)，所以我们直接计算 \((00000000)_{2}\text{~}(01111111)_{2}\) 的 \(\text{popcount}\) 和，也就是 \(0\times 2^{7}+7\times 2^{6}\)。

其第二位为 \(1\)，所以我们直接计算 \((10000000)_{2}\text{~}(10111111)_{2}\) 的 \(\text{popcount}\) 和，也就是 \(1\times 2^{6}+6\times 2^{5}\)。

其第三位是 \(0\)，对答案没有贡献。

其第四位为 \(1\)，所以我们直接计算 \((11000000)_{2}\text{~}(11001111)_{2}\) 的 \(\text{popcount}\) 和，也就是 \(2\times 2^{4}+4\times 2^{3}\)。

其第五位是 \(0\)，对答案没有贡献。

其第六位为 \(1\)，所以我们直接计算 \((11010000)_{2}\text{~}(11010011)_{2}\) 的 \(\text{popcount}\) 和，也就是 \(3\times 2^{2}+2\times 2^{1}\)。

其第七位为 \(1\)，所以我们直接计算 \((11010100)_{2}\text{~}(11010101)_{2}\) 的 \(\text{popcount}\) 和，也就是 \(4\times 2^{1}+1\times 2^{0}\)。

其第八位是 \(0\)，对答案没有贡献。

但其实我们只需要处理 \([0,n)\) 这个区间分段即可。

最后再加上 \(\text{popcount}((11010110)_{2})=5\)。

最终结果就是：

\[0\times 2^{7}+7\times 2^{6}+1\times 2^{6}+6\times 2^{5}+2\times 2^{4}+4\times 2^{3}+3\times 2^{2}+2\times 2^{1}+4\times 2^{1}+1\times 2^{0}+\text{popcount}((11010110)_{2})
\]

\[=448+256+64+16+9+5
\]

\[=798
\]

因为 \(\text{popcount}(0)=0\)，所以统计不统计都可以。

代码

scanf("%d", &n);
long long tot = 0;
int cnt = 0;
int x = n;
while(x)
{
    if(x & 1)
        tot += (cnt * (1 << (cnt - 1))) + (1 << cnt) * __builtin_popcount(x >> 1);
    x >>= 1;
    cnt++;
}
tot += __builtin_popcount(n);
printf("%lld ", tot);

转载自：https://kaiserwilheim.github.io/OI/fast-popcnt-sum/

虽然是转载但是 \(\LaTeX\) 都是我自己打的QAQ