Opencv绘制最小外接矩形、最小外接圆

Opencv中求点集的最小外结矩使用方法minAreaRect，求点集的最小外接圆使用方法minEnclosingCircle。

minAreaRect方法原型：

RotatedRect minAreaRect( InputArray points );

输入参数points是所要求最小外结矩的点集数组或向量；

minEnclosingCircle方法原型：

void minEnclosingCircle( InputArray points,
                                      CV_OUT Point2f& center, CV_OUT float& radius );

第一个参数points是所要求最小外结圆的点集数组或向量；

第二个参数Point2f类型的center是求得的最小外接圆的中心坐标；

第三个参数float类型的radius是求得的最小外接圆的半径；

使用minAreaRect和minEnclosingCircle方法分别求最小外接矩和圆：

<span style="font-size:18px;">#include "core/core.hpp"
#include "highgui/highgui.hpp"
#include "imgproc/imgproc.hpp"
#include "iostream"

using namespace std;
using namespace cv;  

int main(int argc,char *argv[])
{
	Mat imageSource=imread(argv[1],0);
	imshow("Source Image",imageSource);
	Mat image;
	blur(imageSource,image,Size(3,3));
	threshold(image,image,0,255,CV_THRESH_OTSU);
	imshow("Threshold Image",image);

	//寻找最外层轮廓
	vector<vector<Point>> contours;
	vector<Vec4i> hierarchy;
	findContours(image,contours,hierarchy,RETR_EXTERNAL,CHAIN_APPROX_NONE,Point());

	Mat imageContours=Mat::zeros(image.size(),CV_8UC1);	//最小外接矩形画布
	Mat imageContours1=Mat::zeros(image.size(),CV_8UC1); //最小外结圆画布
	for(int i=0;i<contours.size();i++)
	{
		//绘制轮廓
		drawContours(imageContours,contours,i,Scalar(255),1,8,hierarchy);
		drawContours(imageContours1,contours,i,Scalar(255),1,8,hierarchy);

		//绘制轮廓的最小外结矩形
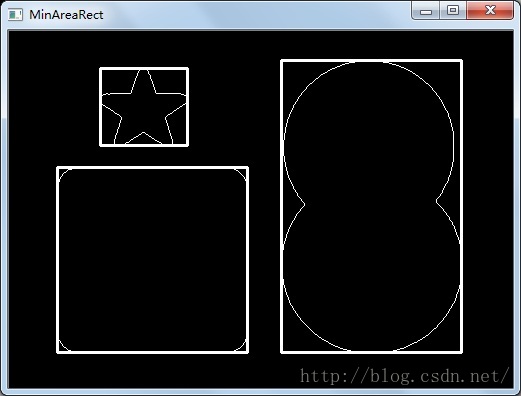
		RotatedRect rect=minAreaRect(contours[i]);
		Point2f P[4];
		rect.points(P);
		for(int j=0;j<=3;j++)
		{
			line(imageContours,P[j],P[(j+1)%4],Scalar(255),2);
		}

		//绘制轮廓的最小外结圆
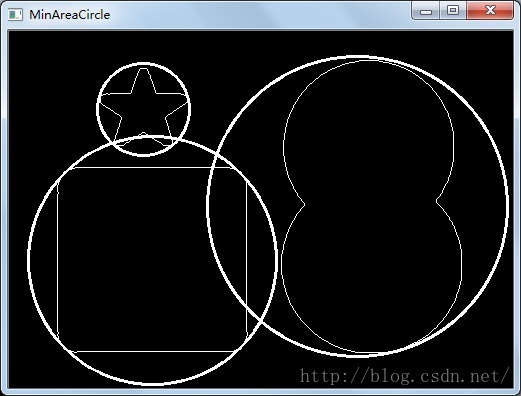
		Point2f center; float radius;
		minEnclosingCircle(contours[i],center,radius);
		circle(imageContours1,center,radius,Scalar(255),2);

	}
	imshow("MinAreaRect",imageContours);
	imshow("MinAreaCircle",imageContours1);
	waitKey(0);
	return 0;
}</span>

作图步骤：

1. 对原始图像均值滤波并二值化；

2. 求图像的最外层轮廓；

3.  使用minAreaRect方法求轮廓的最小外接矩形，转化求得矩形的四个顶点坐标，并绘制矩形；

4.  使用minEnclosingCircle方法求轮廓的最小外接圆，获取圆心和半径信息，并绘制圆；

原始图像：

最小外接矩：

最小外接圆：