乘法器——booth编码

博主最近在学习加法器、乘法器、IEEE的浮点数标准，作为数字IC的基础。当看到booth编码的乘法器时，对booth编码不是很理解，然后在网上找各种理解，终于豁然开朗。现将一个很好的解释分享给大家，希望能对大家有所帮助。

首先，看看这几个公式：

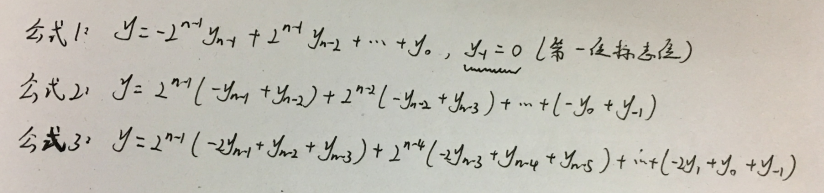
可以证明的是，这三个公式是相等的，一个有符号的二进制数的补码用公式1来表示，可以等价地写成公式2和公式3。

布斯编码可以减少部分积的数目（即减少乘数中1的个数），用来计算有符号乘法，提高乘法运算的速度。

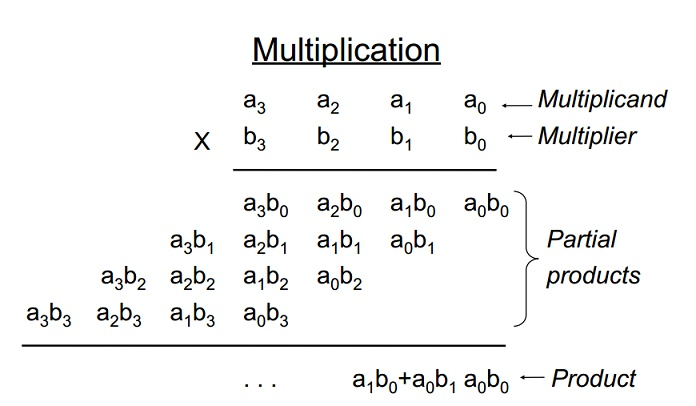
如上图所示为二进制乘法的过程，也是符合我们正常计算时的逻辑，我们假设有一个8位乘数（Multiplier），它的二进制值为0111_1110，它将产生6行非零的部分积，因为它有6个非零值（即1）。如果我们利用公式2将这个二进制值改为1000_00-10，其中低四位中的-1表示负1，可以证明两个值是相等的。可以这样简单理解，那就是现在原值得末尾加辅助位0，变为0111_1110_0，然后利用低位减去高位，即得到1000_00-10。这样一变换可以减少0的数目，从而减少加的次数，我们只需相加两个部分积，但是终的加法器必须也能执行减法。这种形式的变换称为booth encoding（即booth编码），它保证了在每两个连续位中最多只有一个是1或-1。部分积数目的减少意味着相加次数的减少，从而加快了运算速度（并减少了面积）。从形式上来说，这一变换相当于把乘数变换成一个四进制形式。

最经常使用的是改进的booth编码。乘数按三位一组进行划分，相互重叠一位。其实就是把公式1重写为公式3。每一组按下表编码，并形成一个部分积。

    再考虑前面提及的8位二进制数0111_1110。从msb到lsb，可以把它分为三位一组首尾重叠的四组：01（1），11（1），11（1），10（0），末尾补了一个辅助位0。根据上表编码得到：10（2），00（0），00（0），-10（-2），或者表示为1000_000-10，这与前面得到结果是一样的。这时，乘2就是移位。所以布斯算法仅涉及加法，减法和移位操作。

    这样一来就很容易理解了。