sklearn机器学习算法--线性模型

线性模型

• 用于回归的线性模型
• 线性回归（普通最小二乘法）
• 岭回归
• lasso
• 用于分类的线性模型
• 用于多分类的线性模型

1、线性回归

LinearRegression，模型简单，不同调节参数

#2、导入线性回归模型
from sklearn.linear_model import LinearRegression
#3、实例化线性回归模型对象
lr = LinearRegression()
#4、对训练集进行训练
lr.fit(X_train,y_train)
#“斜率”参数（w，也叫作权重或系数）被保存在coef_ 属性中，而偏移或截距（b）被保存在intercept_ 属性中：
print('lr.coef_:{}'.format(lr.coef_))
print('lr.intercept_:{}'.format(lr.intercept_))

2、岭回归

Ridge，调节参数alpha，默认使用L2正则化，alpha越大模型得到的系数就更接近于0，减少alpha可以让系数受到的约束减小。

#导入岭回归模型
from sklearn.linear_model import Ridge
#实例化岭回归模型对象并对训练集进行训练
ridge = Ridge().fit(X_train,y_train)
#查看模型在训练集和测试集上的精确度
print('training score:{}'.format(ridge.score(X_train,y_train)))
print('testing score:{}'.format(ridge.score(X_test,y_test)))
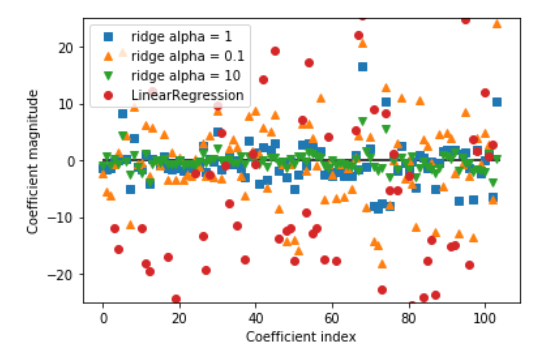
#在实例化Ridge模型中存在参数alpha，alpha越大模型得到的系数就更接近于0，减少alpha可以让系数受到的约束减小。
#比较alpha=0.1,1,10和LinearRegression系数大小
ridge10 = Ridge(alpha=10).fit(X_train, y_train)
ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)

3、Lasso

除了Ridge，还有一种正则化的线性回归是Lasso。与岭回归相同，使用lasso 也是约束系数使其接近于0，但用到的方法不同，叫作L1 正则化。8 L1 正则化的结果是，使用lasso 时某些系数刚好为0。这说明某些特征被模型完全忽略。这可以看作是一种自动化的特征选择。某些系数刚好为0，这样模型更容易解释，也可以呈现模型最重要的特征。

#导入模型
from sklearn.linear_model import Lasso
#实例化模型对象并对训练集进行训练
lasso = Lasso().fit(X_train,y_train)
#查看lasso模型在训练集和测试集上的精度
print('training score:{}'.format(lasso.score(X_train,y_train)))
print('test score:{}'.format(lasso.score(X_test,y_test)))
print('coef number:{}'.format(np.sum(lasso.coef_!=0)))
#发现模型只用到了105 个特征中的4 个。与Ridge 类似，Lasso 也有一个正则化参数alpha，可以控制系数趋向于0 的强度。在上一个例子中，我们用的是默认值alpha=1.0。为了降低欠拟合，我们尝试减小alpha。这么做的同时，我们还需要增加max_iter 的值（运行迭代的最大次数）

4、用于分类的线性模型

最常见的两种线性分类算法是Logistic回归和线性支持向量机（SVM）

#导入Logistic和LinearSVC模型
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
#导入forge数据
X,y = mglearn.datasets.make_forge()
#比较两种模型得到的决策边界
fig,axes = plt.subplots(1,2,figsize = (10,3))
for model,ax in zip([LogisticRegression(),LinearSVC()],axes):
    clf = model.fit(X,y)
    mglearn.plots.plot_2d_separator(clf,X,ax=ax)
    mglearn.discrete_scatter(X[:,0],X[:,1],y,ax=ax)
    ax.set_title(clf.__class__.__name__)
    ax.set_xlabel('Feature 0')
    ax.set_ylabel('Feature 1')

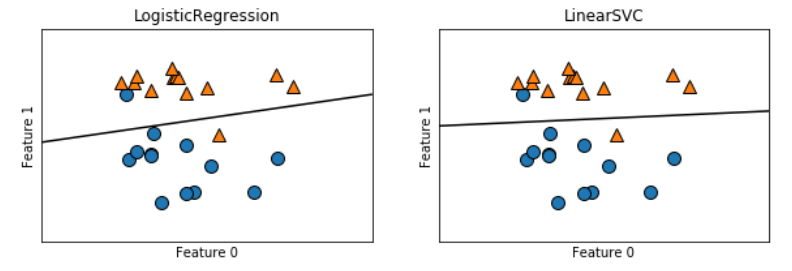
两个模型得到了相似的决策边界。注意，两个模型中都有两个点的分类是错误的。两个模型都默认使用L2 正则化，就像Ridge 对回归所做的那样。对于LogisticRegression 和LinearSVC， 决定正则化强度的权衡参数叫作C。C 值越大，对应的正则化越弱。换句话说，如果参数C 值较大，那么LogisticRegression 和LinearSVC 将尽可能将训练集拟合到最好，而如果C 值较小，那么模型更强调使系数向量（w）接近于0。参数C 的作用还有另一个有趣之处。较小的C 值可以让算法尽量适应“大多数”数据点，而较大的C 值更强调每个数据点都分类正确的重要性。

5、用于多分类线性模型

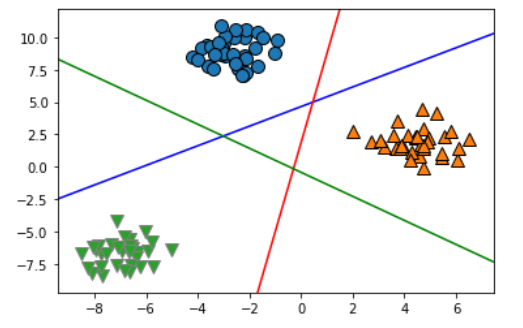
将二分类算法推广到多分类算法的一种常见方法是“一对其余”（one-vs.-rest）方法。在“一对其余”方法中，对每个类别都学习一个二分类模型，将这个类别与所有其他类别尽量分开，这样就生成了与类别个数一样多的二分类模型。在测试点上运行所有二类分类器来进行预测。在对应类别上分数最高的分类器“胜出”，将这个类别标签返回作为预测结果。

#使用正态分布数据演示Logistic多分类模型
#导入高斯分布数据
from sklearn.datasets import make_blobs
X,y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:,0],X[:,1],y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(["Class 0", "Class 1", "Class 2"])
line_svc = LinearSVC().fit(X,y)
mglearn.discrete_scatter(X[:,0],X[:,1],y)
line = np.linspace(-15,15)
for coef, intercept, color in zip(line_svc.coef_,line_svc.intercept_,['b','r','g']):
    plt.plot(line,-(line*coef[0]+intercept)/coef[1],c=color)

总结

在实践中，在Ridge和Lasso两个模型中一般首选岭回归。但如果特征很多，你认为只有其中几个是重要的，那么选择Lasso 可能更好。同样，如果你想要一个容易解释的模型，Lasso 可以给出更容易理解的模型，因为它只选择了一部分输入特征。scikit-learn 还提供了ElasticNet类，结合了Lasso 和Ridge 的惩罚项。在实践中，这种结合的效果最好，不过代价是要调
节两个参数：一个用于L1 正则化，一个用于L2 正则化。线性模型的主要参数是正则化参数，在回归模型中叫作alpha，在LinearSVC 和Logistic-Regression 中叫作C。alpha 值较大或C 值较小，说明模型比较简单。特别是对于回归模型而言，调节这些参数非常重要。通常在对数尺度上对C 和alpha 进行搜索。你还需要确定的是用L1 正则化还是L2 正则化。如果你假定只有几个特征是真正重要的，那么你应该用L1 正则化，否则应默认使用L2 正则化。如果模型的可解释性很重要的话，使用L1 也会有帮助。由于L1 只用到几个特征，所以更容易解释哪些特征对模型是重要的，以及这些特征的作用。