bzoj 1927 [Sdoi2010]星际竞速【最小费用最大流】

果然还是不会建图…

设\( i \)到\( j \)有通路，代价为\( w[i][j] \)，瞬移到i代价为\( a[i] \)，瞬移到i代价为\( a[j] \)，逗号前是流量。



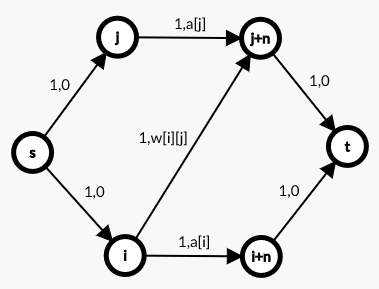
因为每个点只能经过一次，所以流量限制为1，注意到从s开始很难保证出发点不同，所以但是又有联通条件，所以考虑每个扩展过的点（实际不用考虑反正早晚要扩展到）只向外扩展一个点，也就是每次只选两个联通的点（包括瞬移可达）

拆点的作用是加上费用，\( s \)到所有\( i \)连流量1费用0的边，所有\(i \)向t连流量1费用0的边，\( i \)到\( i+n \)连流量1费用\( a[i] \)的边，对于可以相互到达的\( i、j \)，连流量为1费用为\( v[i][j] \)的边（\( u<v \)）

是不是有点像最小路径覆盖？

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int N=5005,inf=1e9;
int n,m,a[N],s,t,ans,fr[N],dis[N],h[N],cnt=1;
bool v[N];
struct qwe
{
	int ne,no,to,va,c;
}e[N*100];
int read()
{
	int r=0,f=1;
	char p=getchar();
	while(p>'9'||p<'0')
	{
		if(p=='-')
			f=-1;
		p=getchar();
	}
	while(p>='0'&&p<='9')
	{
		r=r*10+p-48;
		p=getchar();
	}
	return r*f;
}
void add(int u,int v,int w,int c)
{
	cnt++;
	e[cnt].ne=h[u];
	e[cnt].no=u;
	e[cnt].to=v;
	e[cnt].va=w;
	e[cnt].c=c;
	h[u]=cnt;
}
void ins(int u,int v,int w,int c)
{
	add(u,v,w,c);
	add(v,u,0,-c);
}
bool spfa()
{
	queue<int>q;
	for(int i=s;i<=t;i++)
		dis[i]=inf;
	dis[s]=0;
	v[s]=1;
	q.push(s);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		v[u]=0;
		for(int i=h[u];i;i=e[i].ne)
			if(e[i].va>0&&dis[e[i].to]>dis[u]+e[i].c)
			{
				dis[e[i].to]=dis[u]+e[i].c;
				fr[e[i].to]=i;
				if(!v[e[i].to])
				{
					v[e[i].to]=1;
					q.push(e[i].to);
				}
			}
	}
	return dis[t]!=inf;
}
void mcf()
{
	int x=inf;
	for(int i=fr[t];i;i=fr[e[i].no])
		x=min(x,e[i].va);
	for(int i=fr[t];i;i=fr[e[i].no])
	{
		ans+=x*e[i].c;
		e[i].va-=x;
		e[i^1].va+=x;
	}
}
int main()
{
	n=read(),m=read();
	t=2*n+1;
	for(int i=1;i<=n;i++)
	{
		a[i]=read();
		ins(s,i,1,0);
		ins(i+n,t,1,0);
		ins(s,i+n,1,a[i]);
	}
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read(),w=read();
		if(u>v)
			swap(u,v);
		ins(u,v+n,1,w);
	}
	while(spfa())
		mcf();
	printf("%d\n",ans);
	return 0;
}