编译原理 LR分析（主要是LR（0）分析）

一、LR分析的基本原理

1、LR分析的基本思想

LR方法的基本思想就是，在规范归约的过程中，一方面要记住已移进和归约出的整个字符串，也就是说要记住历史；一方面能够根据所用的产生式的推测未来可能碰到的输入符号，也就是说能够对未来进行展望。这样，当一串貌似句柄的字符串出现在分析栈的顶部时，我们希望能够根据历史和展望以及现实的输入符号这三部分的材料，决定出现在栈顶的这一串符号是否就是我们要找的句柄。

2、LR分析器的构成

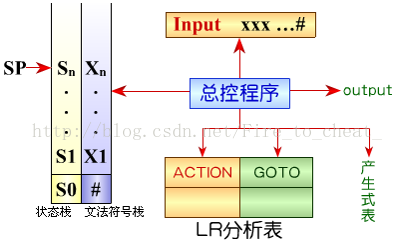
采用下推自动机这种数据模型。包括以下几个部分：

    1.输入带

    2.分析栈：包括状态栈和文法符号栈两部分。(s₀,#)为分析开始前预先放在栈里的初始状态和句子括号。

    3.LR 分析表：包括动作表和状态转移表两张表。

3、LR分析表是LR分析器的核心部分

一张LR分析表包括两部分：动作表(ACTION)和状态转换表(GOTO)。它们都是二维数组。ACTION[s,a]规定了当状态s面临输入符号a时应采取什么动作(移进、归约、接受和报错)，而GOTO[s,X]规定了当状态s面对文法符号X(终结符或非终结符)时的下一状态是什么。

显然， GOTO[s,X]定义了一个以文法符号为字母表的DFA。

不同的 LR 分析法构造LR分析表的方法都不同，由此产生了不同的LR分析法。

4、LR分析算法

置ip指向输入串w的第一个符号

　　令Si为栈顶状态

　　a是ip指向的符号（当前输入符号）

　　BEGIN(重复开始)

　　IFACTION[Si,a]=SjTHEN

BEGIN

PUSH j,a (进栈)

　　　　      ip前进(指向下一输入符号)

　　　    END

　　ELSEIFACTION[Si,a]=rj(若第j条产生式为A→β)
THEN

　　        BEGIN

　　　　      pop|β| 项

　　　　      若当前栈顶状态为Sk

　　　　      pushGOTO[Sk,A] 和A(进栈)

　　　　END

　　ELSEIFACTION[Si,a]=acc THEN

　　　　return (成功）

　　ELSE error

　　END. (重复结束)

二、LR（0）分析器

1、可归前缀与规范句型的活前缀

文法G[S]：
(1) S → aAcBe[1]

(2) A → b[2]

(3) A → Ab[3]

(4) B → d[4]

S ÞaAcBe[1]

ÞaAcd[4]e[1]

ÞaAb[3]cd[4]e[1]

Þab[2]b[3]cd[4]e[1]

每次归约句型的前部分依次为：

ab[2]

aAb[3]

aAcd[4]

aAcBe[1]

规范句型的这种前部分符号串称为可归前缀

我们把形成可归前缀之前包括可归前缀在内的所有规范句型的前缀都称为活前缀

（活前缀就是可归前缀的前缀）如下：

e,a,ab

e ,a,aA,aAb

e ,a,aA,aAc,aAcd

e ,a,aA,aAc,aAcB,aAcBe

三、LR分析

（一）LR分析构造识别活前缀的有穷自动机

项目（item）：在每个产生式的右部适当位置添加一个圆点构成项目。

根据圆点所在的位置和圆点后是终结符还是非终结符把项目分为以下几种：

移进项目，形如 A→a•ab

待约项目，形如 A→a•Bb

归约项目，形如 A→a•

接受项目，形如S’ →S•

根据圆点所在的位置和圆点后是终结符还是非终结符把项目分为以下几种：

移进项目，形如 A →a . ab

    待约项目，形如 A→a . Bb

    归约项目，形如 A→a .

    接受项目，形如 S’→S.

把文法的所有产生式的项目都引出，每个项目都为NFA的一个状态。其中

文法的第一个产生式的第一个项目为文法的初态

文法的接受项目为文法的句子识别态

文法的每一个产生式的归约项目为文法的句柄识别态

构造步骤：

项目圆点的左部表示分析过程的某个时刻用该产生式归约时句柄已识别的部分，圆点右部表示待识别的部分。

构造识别活前缀的NFA：

1、把文法的所有产生式的项目都引出，每个项目都为NFA的一个状态

2、确定、确定状态之间的转换关系

*若项目i为
...Xi-1•
Xi...Xn

项目j为
...Xi-1
Xi •Xi+1...Xn

则从状态i到状态j连一条标记为Xi的箭弧

*若i为X→g•Ad，k为A→•b，则从状态i画标记为
e的箭弧到状态k

（二）将非确定的有限自动机转换成确定的有穷自动机

方法一：（采用子集构造法）

方法二：通过构造文法G的LR（0）的项目集规范族来直接构造识别活前缀的DFA

LR(0)项目集规范族的构造

构成识别一个文法活前缀的DFA项目集（状态）的全体称为这个文法的LR(0)项目集规范族

）通过闭包函数(CLOSURE)来求DFA一个状态的项目集，找出所有的等价的项目。

如果I是文法G’的一个项目集，定义和构造I的闭包CLOSURE(I)如下：
a)I的项目都在CLOSURE(I)中
b)若A→a•
Bb属于CLOSURE(I)，则每一形如B→•
g的项目也属于CLOSURE(I)

c)重复b)直到CLOSURE(I)不再扩大

（2）定义转换函数如下：
GOTO（I，X）=CLOSURE（J）

其中：I为包含某一项目集的状态，X为一文法符号

J={任何形如A→aX •b的项目|A→a•X b属于I}

圆点不在产生式右部最左边的项目称为核，唯一的例外是S’ →
• S。因此用GOTO（I，X）转换函数得到的J为转向后状态所含项目集的核

使用闭包函数（CLOSURE）和转向函数(GOTO(I,X))构造文法G’的LR(0)的项目集规范族，步骤如下：

a)置项目S’→ •S为初态集的核，然后对核求闭包CLOSURE（{S’→
•S}）得到初态的项目集
b)对初态集或其它所构造的项目集应用转换函数GOTO(I，X)=CLOSURE(J)求出新状态J的项目集
c)重复b)直到不出现新的项目集为止