ACM数论之旅8---组合数（组合大法好(,,• ₃ •,,) ）

组合数并不陌生(´・ω・`)

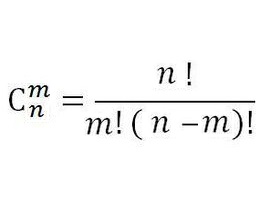
我们都学过组合数

会求组合数吗

一般我们用杨辉三角性质

杨辉三角上的每一个数字都等于它的左上方和右上方的和（除了边界）

第n行，第m个就是，就是C(n, m) （从0开始）

电脑上我们就开一个数组保存，像这样

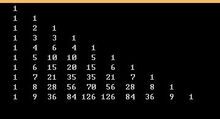
用递推求

 #include<cstdio>
 const int N =  + ;
 const int MOD = (int)1e9 + ;
 int comb[N][N];//comb[n][m]就是C(n,m)
 void init(){
     for(int i = ; i < N; i ++){
         comb[i][] = comb[i][i] = ;
         for(int j = ; j < i; j ++){
             comb[i][j] = comb[i-][j] + comb[i-][j-];
             comb[i][j] %= MOD;
         }
     }
 }
 int main(){
     init();
 }

（PS：大部分题目都要求求余，而且大部分都是对1e9+7这个数求余）

这种方法的复杂度是O(n^2)，有没有O(n)的做法，当然有(´・ω・`)

因为大部分题都有求余，所以我们大可利用逆元的原理（没求余的题目，其实你也可以把MOD自己开的大一点，这样一样可以用逆元做）

根据这个公式

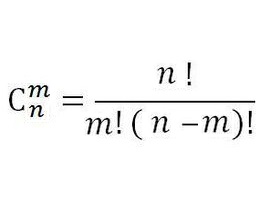
我们需要求阶乘和逆元阶乘

我们就用1e9+7来求余吧

代码如下：

 #include<cstdio>
 const int N =  + ;
 const int MOD = (int)1e9 + ;
 int F[N], Finv[N], inv[N];//F是阶乘，Finv是逆元的阶乘
 void init(){
     inv[] = ;
     for(int i = ; i < N; i ++){
         inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
     }
     F[] = Finv[] = ;
     for(int i = ; i < N; i ++){
         F[i] = F[i-] * 1ll * i % MOD;
         Finv[i] = Finv[i-] * 1ll * inv[i] % MOD;
     }
 }
 int comb(int n, int m){//comb(n, m)就是C(n, m)
     if(m <  || m > n) return ;
     return F[n] * 1ll * Finv[n - m] % MOD * Finv[m] % MOD;
 }
 int main(){
     init();
 }

组合大法好，要懂得善加利用(。-`ω´-)