监督学习——随机梯度下降算法（sgd）和批梯度下降算法（bgd）

线性回归

首先要明白什么是回归。回归的目的是通过几个已知数据来预测另一个数值型数据的目标值。

假设特征和结果满足线性关系，即满足一个计算公式h(x)，这个公式的自变量就是已知的数据x，函数值h(x)就是要预测的目标值。这一计算公式称为回归方程，得到这个方程的过程就称为回归。

假设房子的房屋面积和卧室数量为自变量x，用x1表示房屋面积，x2表示卧室数量；房屋的交易价格为因变量y，我们用h(x)来表示y。假设房屋面积、卧室数量与房屋的交易价格是线性关系。

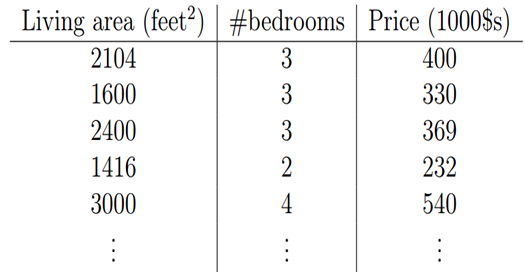
他们满足公式

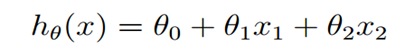
上述公式中的θ为参数，也称为权重，可以理解为x1和x2对h(x)的影响度。对这个公式稍作变化就是

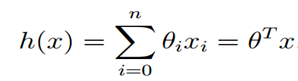
公式中θ和x都可以看成是向量，n是特征数量。

假如我们依据这个公式来预测h(x)，公式中的x是我们已知的（样本中的特征值），然而θ的取值却不知道，只要我们把θ的取值求解出来，我们就可以依据这个公式来做预测了。

最小均方法（Least Mean squares）

在介绍LMS之前先了解一下什么损失函数的概念。

我们要做的是依据我们的训练集，选取最优的θ，在我们的训练集中让h(x)尽可能接近真实的值。h(x)和真实的值之间的差距，我们定义了一个函数来描述这个差距，这个函数称为损失函数，表达式如下：

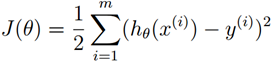
这里的这个损失函数就是著名的最小二乘损失函数，这里还涉及一个概念叫最小二乘法，这里不再展开了。我们要选择最优的θ，使得h(x)最近进真实值。这个问题就转化为求解最优的θ，使损失函数J(θ)取最小值。（损失函数还有其它很多种类型）

那么如何解决这个转化后的问题呢？这又牵扯到一个概念：LMS 和梯度下降（Radient Descent）。

LMS是求取h(x)回归函数的理论依据，通过最小化均方误差来求最佳参数的方法。

梯度下降

我们要求解使得J(θ)最小的θ值，梯度下降算法大概的思路是：我们首先随便给θ一个初始化的值，然后改变θ值让J(θ)的取值变小，不断重复改变θ使J(θ)变小的过程直至J(θ)约等于最小值。

首先我们给θ一个初始值，然后向着让J(θ)变化最大的方向更新θ的取值，如此迭代。公式如下：

公式中α称为步长（learning rate），它控制θ每次向J(θ)变小的方向迭代时的变化幅度。J(θ)对θ的偏导表示J(θ)变化最大的方向。由于求的是极小值，因此梯度方向是偏导数的反方向。

α取值太小收敛速度太慢，太大则可能会Overshoot the minimum。
越接近最小值时，下降速度越慢
收敛: 当前后两次迭代的差值小于某一值时，迭代结束

求解一下这个偏导，过程如下：

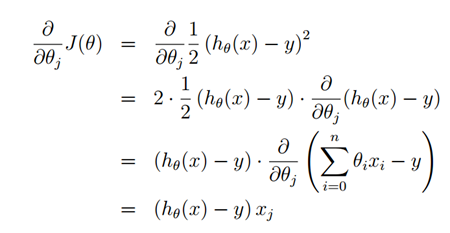
那么θ的迭代公式就变为：

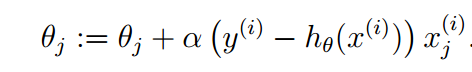
上述表达式只针对样本数量只有一个的时候适用，那么当有m个样本值时该如何计算预测函数？批梯度下降算法和随机梯度下降算法

批梯度下降算法（BGD）

有上一节中单个样本的参数计算公式转化为处理多个样本就是如下表达：

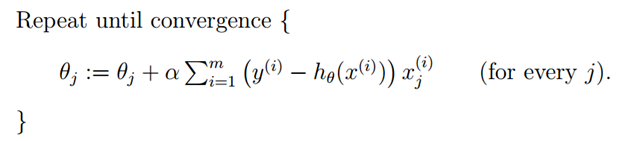
这种新的表达式每一步计算都需要全部训练集数据，所以称之为批梯度下降（batch gradient descent）。

注意，梯度下降可能得到局部最优，但在优化问题里我们已经证明线性回归只有一个最优点，因为损失函数J(θ)是一个二次的凸函数，不会产生局部最优的情况。（假设学习步长α不是特别大）

批梯度下降的算法执行过程如下图：

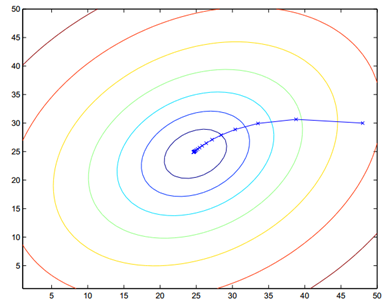
大家仔细看批梯度下降的数学表达式，每次迭代的时候都要对所有数据集样本计算求和，计算量就会很大，尤其是训练数据集特别大的情况。那有没有计算量较小，而且效果也不错的方法呢？有！这就是：随机梯度下降（Stochastic Gradient Descent, SGD）

随机梯度下降算法（SGD）

随机梯度下降在计算下降最快的方向时时随机选一个数据进行计算，而不是扫描全部训练数据集，这样就加快了迭代速度。

随机梯度下降并不是沿着J(θ)下降最快的方向收敛，而是震荡的方式趋向极小点。

随机梯度下降表达式如下：

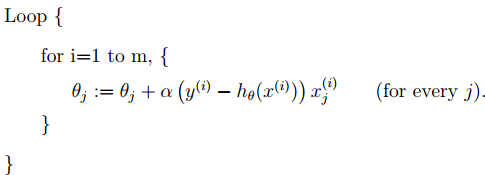
执行过程如下图：

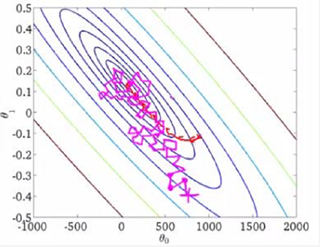
批梯度下降和随机梯度下降在三维图上对比如下：

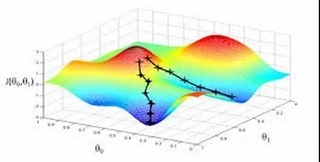
基于梯度下降算法的python3实现如下：(注释部分为BGD的实现)

 # -*- coding: cp936 -*-

 import numpy as np

 from scipy import stats

 import matplotlib.pyplot as plt

 # 构造训练数据

 x = np.arange(0., 10., 0.2)

 m = len(x)                                      # 训练数据点数目

 x0 = np.full(m, 1.0)

 input_data = np.vstack([x0, x]).T               # 将偏置b作为权向量的第一个分量

 target_data = 2 * x + 5 + np.random.randn(m)

 # 两种终止条件

 loop_max = 10000   # 最大迭代次数(防止死循环)

 epsilon = 1e-3

 # 初始化权值

 np.random.seed(0)

 w = np.random.randn(2)

 #w = np.zeros(2)

 alpha = 0.001      # 步长(注意取值过大会导致振荡,过小收敛速度变慢)

 diff = 0.

 error = np.zeros(2)

 count = 0          # 循环次数

 finish = 0         # 终止标志

 # -------------------------------------------随机梯度下降算法----------------------------------------------------------

 while count < loop_max:

     count += 1

     # 遍历训练数据集，不断更新权值

     for i in range(m):

         diff = np.dot(w, input_data[i]) - target_data[i]  # 训练集代入,计算误差值

         # 采用随机梯度下降算法,更新一次权值只使用一组训练数据

         w = w - alpha * diff * input_data[i]

         # ------------------------------终止条件判断-----------------------------------------

         # 若没终止，则继续读取样本进行处理，如果所有样本都读取完毕了,则循环重新从头开始读取样本进行处理。

     # ----------------------------------终止条件判断-----------------------------------------

     # 注意：有多种迭代终止条件，和判断语句的位置。终止判断可以放在权值向量更新一次后,也可以放在更新m次后。

     if np.linalg.norm(w - error) < epsilon:     # 终止条件：前后两次计算出的权向量的绝对误差充分小

         finish = 1

         break

     else:

         error = w

 print ('loop count = %d' % count,  '\tw:[%f, %f]' % (w[0], w[1]))

 # -----------------------------------------------梯度下降法-----------------------------------------------------------

 '''

 while count < loop_max:

     count += 1

     # 标准梯度下降是在权值更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个训练样例来更新的

     # 在标准梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算

     sum_m = np.zeros(2)

     for i in range(m):

         dif = (np.dot(w, input_data[i]) - target_data[i]) * input_data[i]

         sum_m = sum_m + dif     # 当alpha取值过大时,sum_m会在迭代过程中会溢出

     w = w - alpha * sum_m       # 注意步长alpha的取值,过大会导致振荡

     #w = w - 0.005 * sum_m      # alpha取0.005时产生振荡,需要将alpha调小

     # 判断是否已收敛

     if np.linalg.norm(w - error) < epsilon:

         finish = 1

         break

     else:

         error = w

 print ('loop count = %d' % count,  '\tw:[%f, %f]' % (w[0], w[1]))

 '''

 # check with scipy linear regression

 slope, intercept, r_value, p_value, slope_std_error = stats.linregress(x, target_data)

 print ('intercept = %s slope = %s' %(intercept, slope))

 plt.plot(x, target_data, 'k+')

 plt.plot(x, w[1] * x + w[0], 'r')

 plt.show()

总结：

开年第一篇，加油

参考：

http://mp.weixin.qq.com/s/7WlGN8JxfSmpJ8K_EyvgQA

http://m.elecfans.com/article/587673.html