【BZOJ3144】【HNOI2013】切糕

总算做了一道2011以后的省选题了……
原题：

图片题面好评！

P,Q,R≤40，0≤D≤R，给出的所有的不和谐值不超过1000。

文本样例好评！

恩这个是听妹主席讲过后会写的，首先把每个点拆成链，那么割掉这个链上的某条边就表示这个点选了某个权值，边的流量就是这个点设成这个值的花费，表示要花费掉这些代价来把这条边割掉

相邻两个点的值之差<=d怎么搞呐，假设两个相邻的点x，y，那么x的第i个点往y的i-d个点连oo的边，即可，大概就像酱紫：

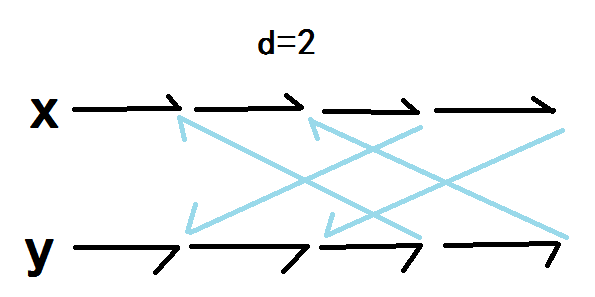
如果有两个被割掉的线段距离超过d，就依然存在一条路径从s到t，就要继续割

差不多是酱紫：

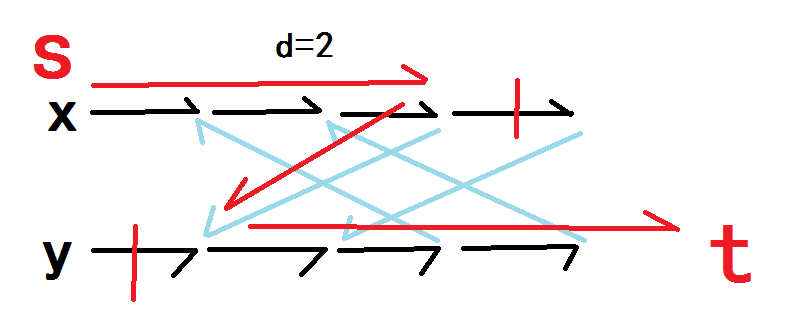
恩就酱

代码：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 using namespace std;
 const int oo=;
 int rd(){int z=,mk=;  char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')mk=-;  ch=getchar();}
     while(ch>=''&&ch<=''){z=(z<<)+(z<<)+ch-'';  ch=getchar();}
     return z*mk;
 }
 struct ddd{int nxt,y,v,rvs;}e[];  int lk[],ltp=;
 inline void ist(int x,int y,int z){
     e[++ltp].nxt=lk[x],lk[x]=ltp,e[ltp].y=y,e[ltp].v=z,e[ltp].rvs=ltp+;
     e[++ltp].nxt=lk[y],lk[y]=ltp,e[ltp].y=x,e[ltp].v=,e[ltp].rvs=ltp-;
 }
 const int fx[]={,-,,},fy[]={,,,-};
 int n,m,h,d;  int N;  int s,t;
 int lvl[];
 int q[],hd=;
 bool gtlvl(){
     memset(lvl,,sizeof(lvl));
     q[hd=]=s,lvl[s]=;
     for(int k=;k<=hd;++k)
         for(int i=lk[q[k]];i;i=e[i].nxt)if(e[i].v && !lvl[e[i].y])
             lvl[e[i].y]=lvl[q[k]]+,q[++hd]=e[i].y;
     return lvl[t];
 }
 int mxflw(int x,int y){
     if(x==t)  return y;
     int bwl=,flw=;
     for(int i=lk[x];i && bwl<y;i=e[i].nxt)if(e[i].v && lvl[e[i].y]==lvl[x]+)
         if((flw=mxflw(e[i].y,min(y-bwl,e[i].v)))){
             bwl+=flw;
             e[i].v-=flw,e[e[i].rvs].v+=flw;
         }
     if(!bwl)  lvl[x]=;
     return bwl;
 }
 int dnc(){
     int bwl=,flw=;
     while(gtlvl())while((flw=mxflw(s,oo)))  bwl+=flw;
     return bwl;
 }
 bool chck(int x,int y,int z){
     return x+fx[z]>= && x+fx[z]<=n && y+fy[z]>= && y+fy[z]<=m;
 }
 inline int gtid(int x,int y,int z){  return z*N+(x-)*m+y;}
 int main(){//freopen("ddd.in","r",stdin);
     cin>>n>>m>>h>>d;  N=n*m;  s=,t=N*(h+)+;
     for(int k=;k<=h;++k)for(int i=;i<=n;++i)for(int j=;j<=m;++j)
         ist(gtid(i,j,k-),gtid(i,j,k),rd());
     for(int i=;i<=n;++i)for(int j=;j<=m;++j)for(int k=;k<;++k)if(chck(i,j,k))
         for(int p=;p+d<=h;++p){
             ist(gtid(i,j,p+d),gtid(i+fx[k],j+fy[k],p),oo);
             ist(gtid(i+fx[k],j+fy[k],p+d),gtid(i,j,p),oo);
         }
     for(int i=;i<=n;++i)for(int j=;j<=m;++j)  ist(s,gtid(i,j,),oo),ist(gtid(i,j,h),t,oo);
     cout<<dnc()<<endl;
     return ;
 }