bzoj 4503

没有权限号就只能对拍了

我们令?代表的T值=0，然后设出这样一个式子

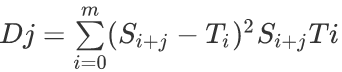
这样一来，只要T和S在j位置匹配，当且仅当Dj=0，然后我们将这个式子拆开，变成下面那样

思路大概就是这样

最后发现答案应该是在ans[lens2-1]---------ans[lens1-1]之间的

翻转字符用FFT优化是一种常见策略

代码：

#include <bits/stdc++.h>
using namespace std;
#define dob complex<double>
const double pi = acos(-1.0);
const int N = 6e4*;
int n, m, l, r[N+], sum[N+],ans[N+];
dob a[N+], b[N+],a1[N+],b1[N+];
void fft(dob *a,int o)
{
    for (int i=;i<n;i++)
      if (i>r[i]) swap(a[i],a[r[i]]);
    for (int i=;i<n;i*=)
    {
        dob wn(cos(pi/i),sin(pi*o/i)),x,y;
        for (int j=;j<n;j+=(i*))
        {
            dob w(,);
            for (int k=;k<i;k++,w*=wn)
            {
                x=a[j+k]; y=w*a[i+j+k];
                a[j+k]=x+y,a[i+j+k]=x-y;
            }
        }
    }
}
char s1[N],s2[N];
void query()
{
    l=;
    for (n = ; n <= m; n <<= ) l++;
    for (int i=;i<n;i++) r[i]=(r[i/]/)|((i&)<<(l-));
    fft(a,),
    fft(b,);
    for (int i=;i<n;i++) a[i]*=b[i];
    fft(a,-);
    for (int i=;i<=m;i++) sum[i]=int (a[i].real()/n+0.5);
}
void clearr()
{
    memset(a,,sizeof(a));
    memset(b,,sizeof(b));
    memset(sum,,sizeof(sum));
}
int main()
{
    freopen("noip.in","r",stdin);
    freopen("noip.out","w",stdout);
    ios::sync_with_stdio(false);
    cin>>s1>>s2;
    for (int i=;i<strlen(s1);i++)
      a1[strlen(s1)-i-]=s1[i]-' ';
    for (int i=;i<strlen(s2);i++)
      if (s2[i]=='?') b[i]=;
      else b1[i]=s2[i]-' ';
    n=max(strlen(s1),strlen(s2)); n--; m=n*;
    clearr();
    for (int i=;i<strlen(s1);i++)
      a[i]=a1[i]*a1[i];
    for (int i=;i<strlen(s2);i++)
      b[i]=b1[i];
//    cout<<b1[0].real();
//    cout<<a1[0].real()<<" "<<a[0].real()<<endl;
    query();
    for (int i=;i<=m;i++) ans[i]+=sum[i];
    clearr();
//    cout<<b1[0].real();
    for (int i=;i<strlen(s1);i++)
      a[i]=a1[i];
    for (int i=;i<strlen(s2);i++)
      b[i]=b1[i]*b1[i];
    query();
    for (int i=;i<=m;i++) ans[i]-=*sum[i];
    int sum2=;
    for (int i=;i<strlen(s2);i++)
      sum2+=pow(b1[i].real(),);
    for (int i=;i<=m;i++)
       ans[i]+=sum2;
    int ans1=;
    for (int i=strlen(s2)-;i<=strlen(s1)-;i++)
      if (!ans[i]) ans1++;
    cout<<ans1<<endl;
}