【题解】UVA10228 A Star not a Tree?

题面传送门

解决思路

本题数据范围较小，可以使用模拟退火算法（随机化）。

顾名思义，模拟退火就是一个类似于降温的过程。先设置一个较大的初温，每次随机改变状态，若使答案更优，则采取更优答案，否则根据其与当前最优答案的差值，一定概率保留这个较不优的答案。这时为了防止答案陷入局部最优的情况:

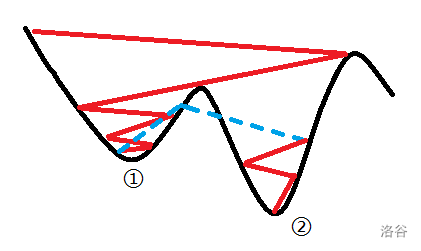
比如下图，陷入局部最优解 \(1\) 的状态后，需要一定的概率跳出来（蓝色虚线），到 \(2\) 处寻找全局最优解。

关于跳出的概率，遵循 『 \(\text{Metropolis}\) 接受准则 』:

设 \(delta=\) 之前最优答案 \(-\) 当前答案，\(T\) 为当前温度。

若 \(p=exp({delta}\div{T})\) 大于 \(\lbrack\ 0,1 )\) 区间的随机数，则仍接受当前状态。

注：\(exp(x)\) 函数：求 \(e\) 的 \(x\) 次方的函数。\(e\) 是一个常数，等于 \(2.718281828…\)

至于为什么，有兴趣可以自己搜索，我们暂且认为这是一种很好的更新方式。

---

那么再看本题，我们就可以用模拟退火的方法不断随机“费马点”的坐标，得到最优解。

说一下退火的一些基本套路：

• 初温一般设为 \(1000\sim3000\)，每次降温的系数一般在 \(0.95\sim0.9975\) 之间，温度下限一般取 \(1e-15\)。可根据数据范围需要和时限做调整。

• 除非你是究极无敌大欧皇，在时间允许情况下，一般建议退火 \(5\sim10\) 次取最优解。

• 对空间类问题，初始的 \(ans\) 一般设为所有点横、纵坐标的平均值。每次调整方法（以横坐标为例）：\(new_x=ans_x+(rand()\times2-\texttt{RAND\_MAX})\times t\)，其中 \(ans_x\) 为之前最优横坐标，\(rand()\times2-\texttt{RAND\_MAX}\) 可以取到 \(-\texttt{RAND\_MAX}\sim \texttt{RAND\_MAX}\) 之间的随机数。乘 \(t\) （当前温度）是为了控制调整幅度。

对于本题，可知 \(ans_x<=max_x\)，\(ans_y<=max_y\)，为了防止刚开始的几次随机到较大的无用结果，我们可以将 \(new_x\) 取模 \(max_x\)，\(new_y\) 取模 \(max_y\)，用 \(fmod()\) 函数即可。

根据笔者试验，在 初温 \(=1000\)，降温系数 \(=0.975\)，退火 \(5\) 次的情况下可以 \(0\ \text{ms}\) 通过本题。

还有，虽然答案要求保留整数，但直接用 \(\text{int}\) 会导致精度丢失。所以都用 \(\text{double}\)，输出答案时四舍五入\((int)(ans+0.5)\) 即可。

最后，注意多测的清空与额外换行！

AC Code：

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0)
#define db double
using namespace std;
db n,ansx,ansy;
db x[105],y[105],ans,mxx,mxy;
int tt,T,ANS;
db dis(db x1,db y1,db x2,db y2){
	db d1=(x1-x2),d2=(y1-y2);
	return sqrt(d1*d1+d2*d2);
}
db calc(db xx,db yy){
	db sum=0;
	for(int i=1;i<=n;i++) sum+=dis(xx,yy,x[i],y[i]);
	return sum;
}
void sa(){
	db t=1000,dw=0.975;
	while(t>1e-15){
		db tx=fmod(ansx+(rand()*2.0-(db)RAND_MAX)*t,mxx);
		db ty=fmod(ansy+(rand()*2.0-(db)RAND_MAX)*t,mxy);
		db m=calc(tx,ty);
		db delta=ans-m;
		if(delta>0) ans=m,ansx=tx,ansy=ty;
		else if((db)rand()<(db)RAND_MAX*(db)exp(delta/t)) ansx=tx,ansy=ty;
		t*=dw;
	}
}
void solve(){
	cin>>n;
	ansx=0,ansy=0;
	for(int i=1;i<=n;i++){
		cin>>x[i]>>y[i];
		mxx=max(mxx,x[i]),mxy=max(mxy,y[i]);
		ansx+=x[i],ansy+=y[i];
	}
	ansx/=n,ansy/=n;
	ans=calc(ansx,ansy);
	tt=5;
	while(tt--) sa();
	cout<<(int)(ans+0.5)<<endl;
	if(T) cout<<endl;
}
int main(){
	IOS;TIE;
	srand(time(NULL));
	cin>>T;
	while(T--) solve();
	return 0;
}