[FJOI2018]领导集团问题

dp[i][j]，i为根子树，最上面的值是j，选择的最大值

观察dp方程

1.整体Dp已经可以做了。

2.考虑优美一些的做法：

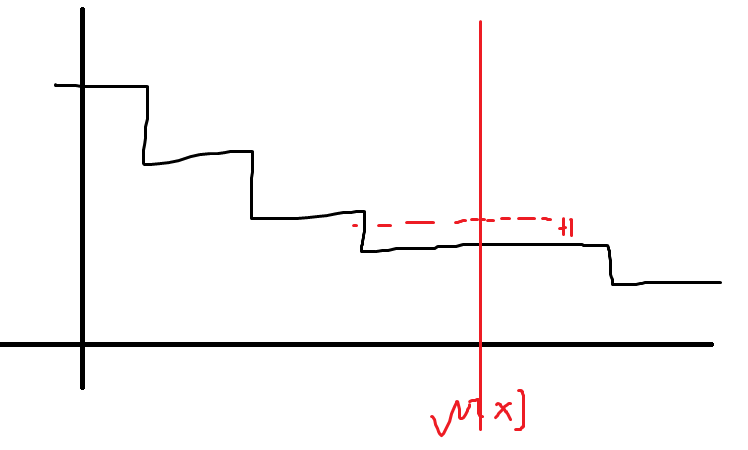
dp[i]如果对j取后缀最大值，显然是不上升的分段函数

而段数就是子树sz

树形Dp的时候，子树之间可以直接把分段函数按位相加。对于<=w[x]的，可以额外获得从dp[i][w[x]]+1得到的转移

1.用map维护，启发式合并，但是合并整体加上一些数不能维护具体值，所以维护差分值！

2.额外转移，找到前驱p，p+1到w[x]整体+1，差分数组上，就是dp[x][w[x]]++,dp[x][p]--

任何时候，如果键值变成0，必须删除。否则第二问就错了。

分段函数、整体Dp都是基于整体上值域个数有限进行的trick

整体Dp运用线段树合并，还可以支持打标记，适用面其实更广。

[九省联考2018]秘密袭击coat

分段函数，通常处理后缀最值，由于单调，通过记录差分数组可以O(1)进行区间加减，启发式合并。如果涉及区间函数平移操作，表现更为灵活。

模拟赛 yjqb

[FJOI2018]领导集团问题的更多相关文章

  1. [FJOI2018]领导集团问题 mulitset合并

    P4577 [FJOI2018]领导集团问题 链接 luogu bzoj 他是个重题 bzoj4919: [Lydsy1706月赛]大根堆 代码改改就过了 思路 求树上的lis,要好好读题目的!!! ...

  2. 【BZOJ5469】[FJOI2018]领导集团问题（动态规划，线段树合并）

    [BZOJ5469][FJOI2018]领导集团问题(动态规划,线段树合并) 题面 BZOJ 洛谷 题解 题目就是让你在树上找一个最大的点集,使得两个点如果存在祖先关系,那么就要满足祖先的权值要小于等 ...

  3. P4577 [FJOI2018]领导集团问题

    P4577 [FJOI2018]领导集团问题 我们对整棵树进行dfs遍历,并用一个multiset维护对于每个点,它的子树可取的最大点集. 我们遍历到点$u$时: 不选点$u$,显然答案就为它的所有子 ...

  4. 5469: [FJOI2018]领导集团问题

    5469: [FJOI2018]领导集团问题 链接 题意: 要求在一棵树内选一个子集,满足子集内的任意两个点u,v,如果u是v的祖先,那么u的权值小于等于v. 分析: dp[u][i]表示在u的子树内 ...

  5. 题解-FJOI2018 领导集团问题

    题面 FJOI2018 领导集团问题 给一棵树 \(T(|T|=n)\),每个点有个权值 \(w_i\),从中选出一个子点集 \(P=\{x\in {\rm node}|x\in T\}\),使得 \ ...

  6. 「题解报告」P4577 [FJOI2018]领导集团问题

    题解 P4577 [FJOI2018]领导集团问题 题解区好像没有线段树上又套了二分的做法,于是就有了这片题解. 题目传送门 怀着必 WA 的决心交了两发,一不小心就过了. 题意 求一个树上最长不下降 ...

  7. 洛谷P4577 [FJOI2018]领导集团问题(dp 线段树合并)

    题意 题目链接 Sol 首先不难想到一个dp,设\(f[i][j]\)表示\(i\)的子树内选择的最小值至少为\(j\)的最大个数 转移的时候维护一个后缀\(mx\)然后直接加 因为后缀max是单调不 ...

  8. 洛谷4577 & LOJ2521：[FJOI2018]领导集团问题——题解

    https://www.luogu.org/problemnew/show/P4577 https://loj.ac/problem/2521 参考:https://www.luogu.org/blo ...

  9. bzoj5469 [FJOI2018]领导集团问题

    题目描述: bz luogu 题解: 相当于树上$LIS$问题. 考虑一维情况下的贪心,我们可以用multiset启发式合并搞. 代码: #include<set> #include< ...

随机推荐

  1. js实现横向跑马灯效果

    首先我们需要一个html代码的框架如下: <div style="position: absolute; top: 0px; left: 168px; width: 100%; mar ...

  2. javaweb学习--jsp

    阅读电子书<Java Web从入门到精通>密码:461c,学习JavaWeb基础知识.由于本人已有html基础,所以直接略过前面部分,进入jsp学习 jsp页面添加库引用,引入项目文件 引 ...

  3. local_irq_disable和disable_irq的区别

    local_irq_disable: local_irq_disable的功能是屏蔽当前CPU上的所有中断,通过操作arm核心中的寄存器来屏蔽到达CPU上的中断,此时中断控制器中所有送往该CPU上的中 ...

  4. c/c++ llinux epoll系列4 利用epoll_wait实现非阻塞的connect

    llinux epoll系列4 利用epoll_wait实现非阻塞的connect connect函数是阻塞的,而且不能设置connect函数的timeout时间,所以一旦阻塞太长时间,影响用户的体验 ...

  5. mybatis使用oracle的sequence

    oracle数据库创建SEQUENCE CREATE SEQUENCE SEQ_COM_MASTER START INCREMENT MINVALUE MAXVALUE NOCYCLE CACHE ; ...

  6. 3星|《HBO的内容战略》：HBO与美国电视业大事记

    HBO的内容战略 基本是HBO与美国电视业的大事记.从电视的诞生讲起.HBO在1972年首播,1975年做出一个当时惊世骇俗的决定:勇卫星实时向全美发送信号,随即成为覆盖全国的电视台:80年代受到录像 ...

  7. Python中的一些小技巧

    1.Boolean值可以当做一个数值 a = [5,6,7,8,9] print(a[True]) #prints 6 print(a[False]) #prints 5 2.两种方法实现 a = 1 ...

  8. 软件设计之Deep Module（深模块）

    类是不是越小越好?最近在读John Ousterhout的<A Philosophy of Software Design>,感到作者文笔流畅,书中内容具有启发性.这里摘要一部分内容,以供 ...

  9. day4-python基础-小数据池以及深浅copy浅讲

    今天的目录是 1.小数据池 2.深浅copy 正文开始 1.小数据池 在说明今天的内容前,先说明一个在今天重复用到的一个知识点 ###比较’=’俩边的数据是否完全相同,以及判断一个对象的内存地址是否完 ...

  10. app原生和H5混合使用自动化

    1.从原生切换到H5需要 driver.switch_to.context('WEBVIEW_com.tencent.mm:tools') 2.参考连接: https://testerhome.com ...