【BZOJ4300】绝世好题（二进制，DP）

题意：

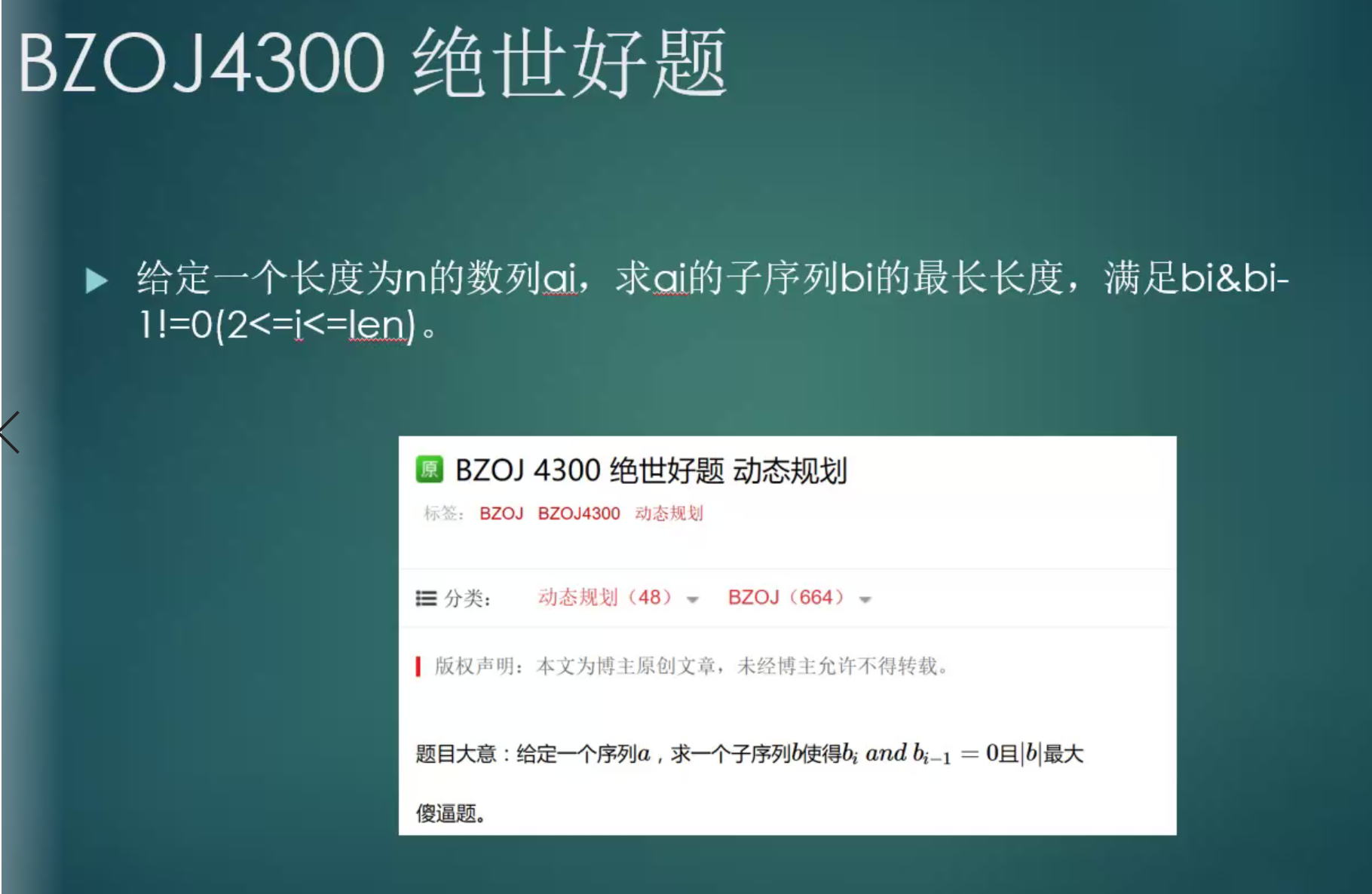
n<=100000,ai<=2*10^9

思路：按二进制逐位考虑，只要有至少1位取and后为1就可以接下去

设dp[i]为第i位取and之后为1的最长的序列长度，意会一下

 #include<cstdio>
 #include<iostream>
 typedef long long ll;
 using namespace std;
 #define MOD 1000000007
 #define N 110000
 int a[N],dp[];

 int main()
 {
     int n;
     scanf("%d",&n);
     for(int i=;i<=n;i++) scanf("%d",&a[i]);
     for(int i=;i<=n;i++)
     {
         int tmp=;
         for(int j=;j<=;j++)
          if(a[i]&(<<(j-))) tmp=max(tmp,dp[j]);
         tmp++;
         for(int j=;j<=;j++)
          if(a[i]&(<<(j-))) dp[j]=max(dp[j],tmp);
     }
     int ans=;
     for(int i=;i<=;i++) ans=max(ans,dp[i]);
     printf("%d\n",ans);
     return ;
 }