Expm 4_2 有向无环图中的最短路径问题

【问题描述】

建立一个从源点S到终点E的有向无环图，设计一个动态规划算法求出从S到E的最短路径值，并输出相应的最短路径。

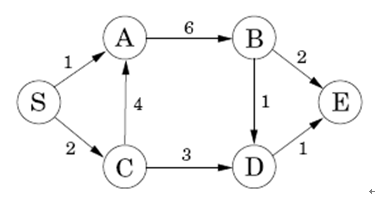
解：

 package org.xiu68.exp.exp4;

 import java.util.ArrayDeque;
 import java.util.Stack;

 public class Exp4_2 {
     //建立一个从源点S到终点E的有向无环图，设计一个动态规划算法求出从S到E的最短路径值，并输出相应的最短路径。
     public static void main(String[] args) {
         int m=Integer.MAX_VALUE;
         int[][] edges=new int[][]{
             {m,1,m,2,m,m},
             {m,m,6,m,m,m},
             {m,m,m,m,1,2},
             {m,4,m,m,3,m},
             {m,m,m,m,m,1},
             {m,m,m,m,m,m}
         };
         MGraph1 m1=new MGraph1(edges);
         m1.minPath(0, 5);
         //输出
         //  0 to 5 is 6
         // the path is:0-->3-->4-->5

     }
 }

 class MGraph1{
     private int[][] edges;        //有向无环图
     private int    vexNum;            //顶点数量

     public MGraph1(int[][] edges){
         this.edges=edges;
         this.vexNum=edges.length;
     }

     public void minPath(int start,int end){

         int[] dist=new int[vexNum];            //源点到该点的最短路径
         for(int i=0;i<vexNum;i++)
             dist[i]=Integer.MAX_VALUE;
         dist[start]=0;

         int[] pre=new int[vexNum];            //最短路径中该点的前一个顶点
         pre[start]=-1;

         Stack<Integer> queue=new Stack<>();    //存放拓扑排序序列
         topoSort(queue);

         while(!queue.isEmpty()){
             int j=queue.pop();

             for(int i=0;i<vexNum;i++){
                 if(edges[i][j]!=Integer.MAX_VALUE && dist[j]>dist[i]+edges[i][j]){
                     dist[j]=dist[i]+edges[i][j];
                     pre[j]=i;
                 }
             }//for
         }//while

         //打印最短路径
         System.out.println(start+" to "+end+" is "+dist[end]);

         String path=""+end;
         int preVex=pre[end];

         while(preVex!=-1){
             path=preVex+"-->"+path;
             preVex=pre[preVex];
         }
         System.out.println("the path is:"+path);

     }

     //拓扑排序
     public void topoSort(Stack<Integer> queue){
         boolean[] visited=new boolean[vexNum];
         for(int i=0;i<vexNum;i++){
             if(!visited[i])
                 dfs(queue,i,visited);
         }
     }

     //利用深度优先搜索进行拓扑排序
     public void dfs(Stack<Integer> queue,int v,boolean[] visited){
         visited[v]=true;
         for(int i=0;i<vexNum;i++){
             if(edges[v][i]!=Integer.MAX_VALUE && !visited[i])
                 dfs(queue,i,visited);
         }
         queue.push(v);
     }
 }