MKL库线性方程组求解(LAPACKE_?gesv)

LAPACK（Linear Algebra PACKage）库，是用Fortran语言编写的线性代数计算库，包含线性方程组求解（\(AX=B\)）、矩阵分解、矩阵求逆、求矩阵特征值、奇异值等。该库用BLAS库做底层运算。

本示例将使用MKL中的LAPACK库计算线性方程组\(AX=B\)的解，并扩展使用此思路求逆矩阵的过程。首先介绍原理部分：

LU分解

引用自 LU分解 - 维基百科

对于方阵\(A\)，其\(LU\)分解是将它分解成一个下三角矩阵\(L\)与上三角矩阵\(U\)的乘积，即\(A=LU\)，

如一个\(3 \times 3\)的矩阵\(A\) ，其\(LU\)分解会写成下面的形式：

\[{\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{bmatrix}}={\begin{bmatrix}l_{11}&0&0\\l_{21}&l_{22}&0\\l_{31}&l_{32}&l_{33}\\\end{bmatrix}}{\begin{bmatrix}u_{11}&u_{12}&u_{13}\\0&u_{22}&u_{23}\\0&0&u_{33}\\\end{bmatrix}}}{\displaystyle }\\
A\vec x = \vec b \Leftrightarrow (LU)\vec x = \vec b \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{L\vec y = \vec b}\\
{U\vec x = \vec y}
\end{array}} \right.
\]

分解之后，由于\(L\)与\(U\)分别为下、上三角矩阵，再去求解\(X\)将变得更加简单。

然而，\(LU\)分解只适用于能用消去法处理的矩阵（比如左上角第一个元素为0时就无法消去）。

而\(PLU\)分解在加入置换矩阵\(P\)进行换行后，便可对任意实矩阵进行\(LU\)分解，此时\(A=P*L*U\)。

LAPACKE_sgesv计算线性方程组\(A*X = B\) 的解，其中 \(A\) 是$ N×N$ 矩阵，\(X\) 和 \(B\) 是 \(N×NRHS\) 矩阵。 将 \(A\) 分解为 \(A = P * L * U\)，其中 \(P\) 是置换矩阵，\(L\)是单位下三角矩阵，\(U\)是上三角矩阵。 然后使用\(A\)的分解式来求解方程组\(A * X = B\)。

1 参数详解

lapack_int LAPACKE_sgesv( matrix_layout, 	// (input) 行优先(LAPACK_ROW_MAJOR)或列优先(LAPACK_COL_MAJOR)
                         n,			// (input) 线性方程的个数,n>=0
                         nrhs,			// (input) 矩阵B的列数，即线性方程组右端的项个数,nrhs>=0
                         a, 			// (input/output)系数矩阵A，维度为nxn
                         lda, 			// (input) A矩阵的第一维
                         ipiv,			// (output) 置换矩阵，ipiv[i]表示矩阵A的第i行与第ipiv[i]行进行了交换
                         b,			// (input/output)B矩阵
                         ldb 			// (input) B矩阵的第一维
                        );

2 定义线性方程组

Intel给出的官方示例为：

\[A = \left[ {\begin{array}{*{20}{r}}
{6.80}&{ - 6.05}&{ - 0.45}&{8.32}&{ - 9.67}\\
{ - 2.11}&{ - 3.30}&{2.58}&{2.71}&{ - 5.14}\\
{5.66}&{5.36}&{ - 2.70}&{4.35}&{ - 7.26}\\
{5.97}&{ - 4.44}&{0.27}&{ - 7.17}&{6.08}\\
{8.23}&{1.08}&{9.04}&{2.14}&{ - 6.87}
\end{array}} \right]~~~~~B = \left[ {\begin{array}{*{20}{r}}
{4.02}&{ - 1.56}&{9.81}\\
{6.19}&{4.00}&{ - 4.09}\\
{ - 8.22}&{ - 8.67}&{ - 4.57}\\
{ - 7.57}&{1.75}&{ - 8.61}\\
{ - 3.03}&{2.86}&{8.99}
\end{array}} \right]
\]

去求解\(AX=B\)的解\(X\)。

#include <stdlib.h>
#include <stdio.h>
#include "mkl_lapacke.h"

// 参数
#define N 5
#define NRHS 3
#define LDA N
#define LDB NRHS

MKL_INT n = N, nrhs = NRHS, lda = LDA, ldb = LDB, info;

MKL_INT ipiv[N];
float a[LDA*N] = {
    6.80f, -6.05f, -0.45f,  8.32f, -9.67f,
    -2.11f, -3.30f,  2.58f,  2.71f, -5.14f,
    5.66f, 5.36f, -2.70f,  4.35f, -7.26f,
    5.97f, -4.44f,  0.27f, -7.17f, 6.08f,
    8.23f, 1.08f,  9.04f,  2.14f, -6.87f
};
float b[LDB*N] = {
    4.02f, -1.56f, 9.81f,
    6.19f,  4.00f, -4.09f,
    -8.22f, -8.67f, -4.57f,
    -7.57f,  1.75f, -8.61f,
    -3.03f,  2.86f, 8.99f
};

3 执行求解过程

LAPACKE_sgesv( LAPACK_ROW_MAJOR, n, nrhs, a, lda, ipiv, b, ldb );

输出结果为：

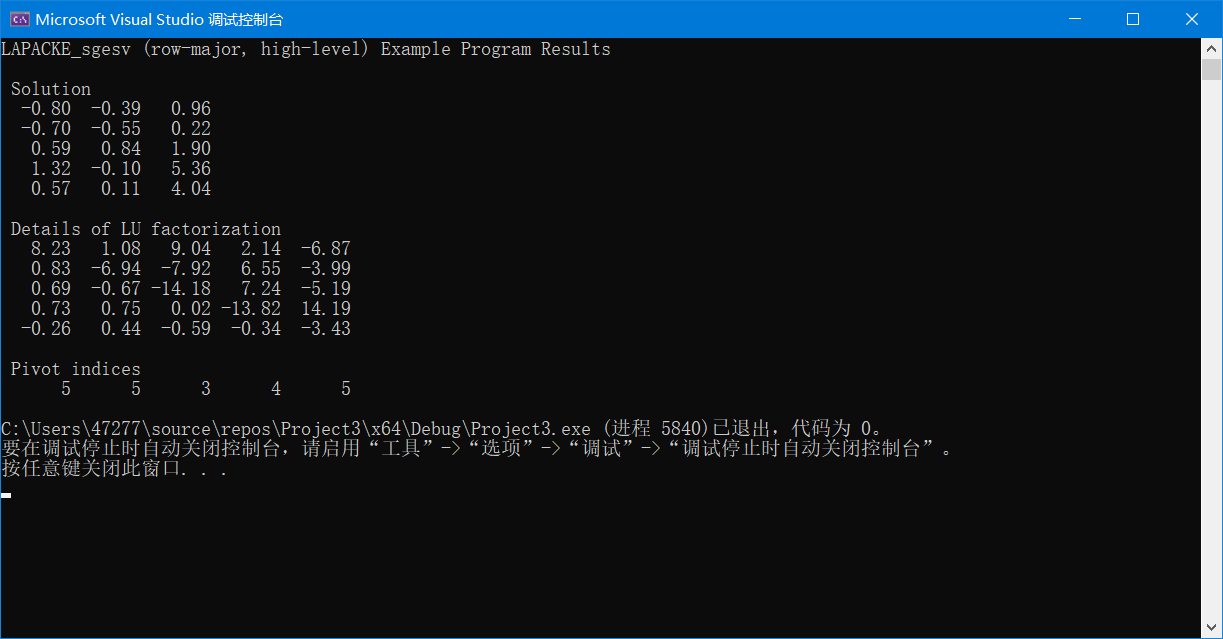
完整代码

#include <stdlib.h>
#include <stdio.h>
#include "mkl_lapacke.h"

extern void print_matrix(const char* desc, MKL_INT m, MKL_INT n, float* a, MKL_INT lda);
extern void print_int_vector(const char* desc, MKL_INT n, MKL_INT* a);

#define N 5
#define NRHS 3
#define LDA N
#define LDB NRHS

int main() {

    MKL_INT n = N, nrhs = NRHS, lda = LDA, ldb = LDB, info;

    MKL_INT ipiv[N];
    float a[LDA * N] = {
        6.80f, -6.05f, -0.45f,  8.32f, -9.67f,
       -2.11f, -3.30f,  2.58f,  2.71f, -5.14f,
        5.66f, 5.36f, -2.70f,  4.35f, -7.26f,
        5.97f, -4.44f,  0.27f, -7.17f, 6.08f,
        8.23f, 1.08f,  9.04f,  2.14f, -6.87f
    };
    float b[LDB * N] = {
        4.02f, -1.56f, 9.81f,
        6.19f,  4.00f, -4.09f,
       -8.22f, -8.67f, -4.57f,
       -7.57f,  1.75f, -8.61f,
       -3.03f,  2.86f, 8.99f
    };

    printf("LAPACKE_sgesv (row-major, high-level) Example Program Results\n");

    info = LAPACKE_sgesv(LAPACK_ROW_MAJOR, n, nrhs, a, lda, ipiv,
        b, ldb);

    if (info > 0) {
        printf("The diagonal element of the triangular factor of A,\n");
        printf("U(%i,%i) is zero, so that A is singular;\n", info, info);
        printf("the solution could not be computed.\n");
        exit(1);
    }

    print_matrix("Solution", n, nrhs, b, ldb);

    print_matrix("Details of LU factorization", n, n, a, lda);

    print_int_vector("Pivot indices", n, ipiv);
    exit(0);
} 

void print_matrix(const char* desc, MKL_INT m, MKL_INT n, float* a, MKL_INT lda) {
    MKL_INT i, j;
    printf("\n %s\n", desc);
    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++) printf(" %6.2f", a[i * lda + j]);
        printf("\n");
    }
}

void print_int_vector(const char* desc, MKL_INT n, MKL_INT* a) {
    MKL_INT j;
    printf("\n %s\n", desc);
    for (j = 0; j < n; j++) printf(" %6i", a[j]);
    printf("\n");
}

补充：矩阵求逆

简单来说，在使用以上API计算\(AX=B\)，当\(B\)为单位矩阵时，\(X\)即为\(A^{-1}\)。

将上述案例中的

float b[LDB * N] = {
    4.02f, -1.56f, 9.81f,
    6.19f,  4.00f, -4.09f,
    -8.22f, -8.67f, -4.57f,
    -7.57f,  1.75f, -8.61f,
    -3.03f,  2.86f, 8.99f
};
/**********改为**********/

#define NRHS 5
float b[LDB * N] = {
    1.0f, 0.0f, 0.0f, 0.0f, 0.0f,
    0.0f, 1.0f, 0.0f, 0.0f, 0.0f,
    0.0f, 0.0f, 1.0f, 0.0f, 0.0f,
    0.0f, 0.0f, 0.0f, 1.0f, 0.0f,
    0.0f, 0.0f, 0.0f, 0.0f, 1.0f,
};

即可求解矩阵\(A\)的逆矩阵，输出为：

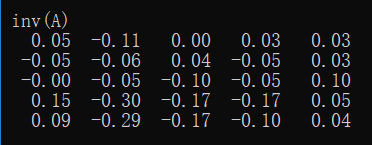
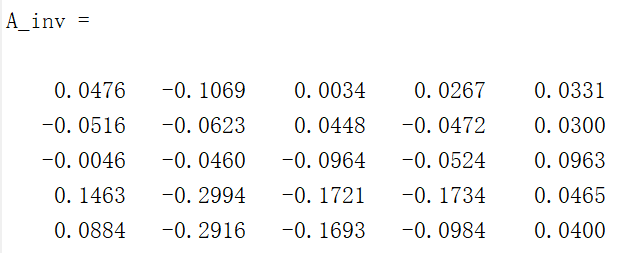
对比在Matlab中使用inv()函数求逆：

A = [ 6.80, -6.05, -0.45,  8.32, -9.67;
     -2.11, -3.30,  2.58,  2.71, -5.14;
      5.66,  5.36, -2.70,  4.35, -7.26;
      5.97, -4.44,  0.27, -7.17,  6.08;
      8.23,  1.08,  9.04,  2.14, -6.87];
A_inv=inv(A)

结果相同。