verilog 实现加法器

半加器

如果不考虑来自低位的进位将两个1二进制数相加，称为半加。

实现半加运算的逻辑电路称为半加器。

真值表

>> 逻辑表达式和
\begin{align}\notag
s = a{b}' + {a}'b
\end{align}
>> 逻辑表达式进位输出
\begin{align}\notag
co = ab
\end{align}

verilog code

module halfadder(
                 output       s,  //sum
                 output       co, //carry
                 input        a,
                 input        b
                 );

assign    s  = a ^ b;
assign    co = a & b;
//assign     {co,s} = a + b;

endmodule

testbench

module halfadder_tb;

wire  s;
wire  co;
reg   a;
reg   b;

initial
begin
    a = 0;
    b = 0;
    #10 a = 0 ;b = 0;
    #10 a = 0 ;b = 1;
    #10 a = 1 ;b = 0;
    #10 a = 1 ;b = 1;
    #10 $finish;
end

initial begin
  $fsdbDumpfile("test.fsdb");
  $fsdbDumpvars();
end

halfadder u_halfadder(
                      .s(s),
                      .co(co),
                      .a(a),
                      .b(b)
                      );

endmodule

---

全加器

在将两位多位二进制数相加时，除了最低位以外，每位都应该考虑来自低位的进位，即将两个对应位的加数和来自低位的进位3个数相加。这种运算称为全加，所用的电路称为全加器。

真值表

逻辑表达式和

\begin{align}\notag
s = {({a}'{b}'{ci}' + a{b}'ci + {a}'bci + ab{ci}'})'
\end{align}
>> 逻辑表达式进位输出
\begin{align}\notag
co = {({a}'{b}' + {b}'{ci}' + {a}'{ci}')}'
\end{align}

verilog code

module fulladder(
                 output       s,  //sum
                 output       co, //carry to high bit
                 input        a,
                 input        b,
                 input        ci  //carry from low bit
                 );
//RTL level
assign s  = ~((~a&~b&~ci)||(a&~b&ci)||(~a&b&ci)||(a&b&~ci));
assign co = ~((~a&~b)||(~b&~ci)||(~a&~ci));

//assign {co,s} = a + b + ci;

endmodule

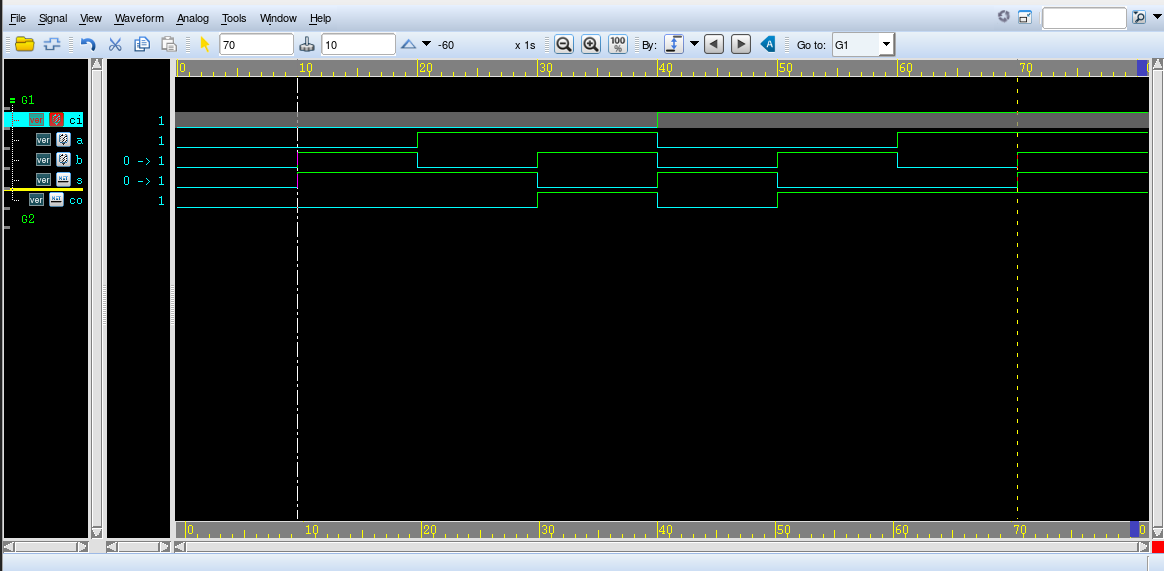
testbench

module fulladder_tb;

wire  s;
wire  co;
reg   a;
reg   b;
reg   ci;

initial
begin
        ci = 0; a = 0 ;b = 0;
    #10 ci = 0; a = 0 ;b = 1;
    #10 ci = 0; a = 1 ;b = 0;
    #10 ci = 0; a = 1 ;b = 1;
    #10 ci = 1; a = 0 ;b = 0;
    #10 ci = 1; a = 0 ;b = 1;
    #10 ci = 1; a = 1 ;b = 0;
    #10 ci = 1; a = 1 ;b = 1;
    #10 $finish;
end

initial begin
  $fsdbDumpfile("test.fsdb");
  $fsdbDumpvars();
end

fulladder u_fulladder(
                      .s(s),
                      .co(co),
                      .a(a),
                      .b(b),
                      .ci(ci)
                      );

endmodule

---

多位加法器

串行进位加法器

依次将低位全加器的进位输出co接到全加器的进位输入端ci，就可以构成多位加法器。

显然，每一位的相加结果都必须等到低一位的进位产生才能建立起来，因此，这种结构的电路称为串行进位加法器（或称为行波进位加法器）。

verilog code (fulladder为上面所述的全加器)

module serialadder(
                   output   [3:0]   s,
                   output           co,
                   input    [3:0]   a,
                   input    [3:0]   b,
                   input            ci
                   );
wire   [3:0]   co_tmp;

fulladder   u_add0(
                   .s(s[0]),  //sum
                   .co(co_tmp[0]), //carry to high bit
                   .a(a[0]),
                   .b(b[0]),
                   .ci(ci)  //carry from low bit
                   );

fulladder   u_add1(
                   .s(s[1]),  //sum
                   .co(co_tmp[1]), //carry to high bit
                   .a(a[1]),
                   .b(b[1]),
                   .ci(co_tmp[0])  //carry from low bit
                   );

fulladder   u_add2(
                   .s(s[2]),  //sum
                   .co(co_tmp[2]), //carry to high bit
                   .a(a[2]),
                   .b(b[2]),
                   .ci(co_tmp[1])  //carry from low bit
                   );

fulladder   u_add3(
                   .s(s[3]),  //sum
                   .co(co_tmp[3]), //carry to high bit
                   .a(a[3]),
                   .b(b[3]),
                   .ci(co_tmp[2])  //carry from low bit
                   );

assign   co = co_tmp[3];

endmodule

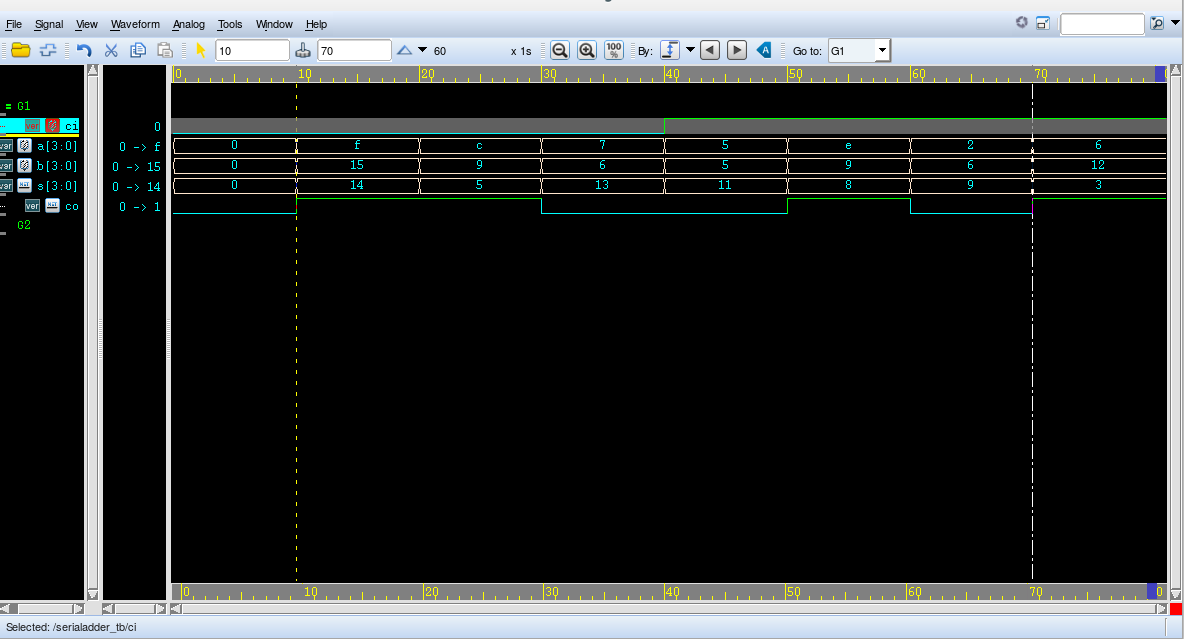
testbench

module serialadder_tb;
wire      [3:0]       s;
wire                  co;
reg       [3:0]       a;
reg       [3:0]       b;
reg                   ci;

initial
begin
          a = 4'b0000; b = 4'b0000; ci = 0;
    #10   a = 4'b1111; b = 4'b1111; ci = 0;
    #10   a = 4'b1100; b = 4'b1001; ci = 0;
    #10   a = 4'b0111; b = 4'b0110; ci = 0;
    #10   a = 4'b0101; b = 4'b0101; ci = 1;
    #10   a = 4'b1110; b = 4'b1001; ci = 1;
    #10   a = 4'b0010; b = 4'b0110; ci = 1;
    #10   a = 4'b0110; b = 4'b1100; ci = 1;
    #10   $finish;
end

initial begin
  $fsdbDumpfile("test.fsdb");
  $fsdbDumpvars();
end

serialadder u_serialadder(
                          .s(s),
                          .co(co),
                          .a(a),
                          .b(b),
                          .ci(ci)
                          );

endmodule

---

超前进位加法器

超前进位信号的产生原理

• ab = 1 --> co = 1
• a + b = 1,且ci = 1 --> co =1

两位多位数中第i位相加产生的进位输出co(i)可以表示位

\begin{align}\notag
co_{i} = a_{i}b_{i} + (a_{i} + b_{i})(ci_{i})
\end{align}

>> 从全加器的真值表写出第i位和s(i)的逻辑式：
\begin{align}\notag
s_{i} = a_{i}{b_{i}}'{ci_{i}}' + {a_{i}}'b_{i}{ci_{i}}' + {a_{i}}'{b_{i}}'ci_{i} + (a_{i} + b_{i})ci_{i}
\end{align}
>> 上式变换位异或函数位：
\begin{align}\notag
s_{i} = a_{i} \oplus b_{i} \oplus ci_{i}
\end{align}

verilog code

module carry_look_aheadadder(
                             output     [3:0]   s,
                             output             co,
                             input      [3:0]   a,
                             input      [3:0]   b,
                             input              ci
                             );
wire  [3:0]    co_tmp;
wire  [3:0]    cin;

assign  cin[3:0]  = {co_tmp[2:0],ci};

//计算中间进位
assign  co_tmp[0] = a[0]&b[0] || (a[0] || b[0])&(cin[0]);
assign  co_tmp[1] = a[1]&b[1] || (a[1] || b[1])&(cin[1]);
assign  co_tmp[2] = a[2]&b[2] || (a[2] || b[2])&(cin[2]);
assign  co_tmp[3] = a[3]&b[3] || (a[3] || b[3])&(cin[3]);

//计算和
assign s[0] = a[0] ^ b[0] ^ cin[0];
assign s[1] = a[1] ^ b[1] ^ cin[1];
assign s[2] = a[2] ^ b[2] ^ cin[2];
assign s[3] = a[3] ^ b[3] ^ cin[3];

assign co = co_tmp[3];
endmodule

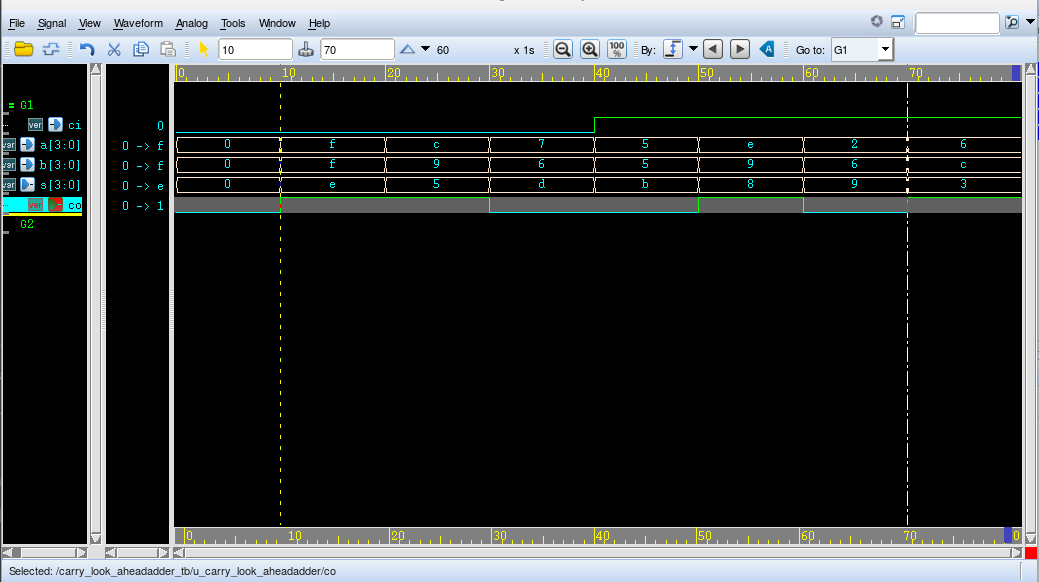
testbench

module carry_look_aheadadder_tb;
wire      [3:0]       s;
wire                  co;
reg       [3:0]       a;
reg       [3:0]       b;
reg                   ci;

initial
begin
          a = 4'b0000; b = 4'b0000; ci = 0;
    #10   a = 4'b1111; b = 4'b1111; ci = 0;
    #10   a = 4'b1100; b = 4'b1001; ci = 0;
    #10   a = 4'b0111; b = 4'b0110; ci = 0;
    #10   a = 4'b0101; b = 4'b0101; ci = 1;
    #10   a = 4'b1110; b = 4'b1001; ci = 1;
    #10   a = 4'b0010; b = 4'b0110; ci = 1;
    #10   a = 4'b0110; b = 4'b1100; ci = 1;
    #10   $finish;
end

initial begin
  $fsdbDumpfile("test.fsdb");
  $fsdbDumpvars();
end

carry_look_aheadadder u_carry_look_aheadadder(
                                              .s(s),
                                              .co(co),
                                              .a(a),
                                              .b(b),
                                              .ci(ci)
                                              );

endmodule

参考资料

[1] 数字电子技术基础(第五版) 阎石主编