回归模型效果评估系列3-R平方

决定系数（coefficient of determination，R2）是反映模型拟合优度的重要的统计量，为回归平方和与总平方和之比。R2取值在0到1之间，且无单位，其数值大小反映了回归贡献的相对程度，即在因变量Y的总变异中回归关系所能解释的百分比。 R2是最常用于评价回归模型优劣程度的指标，R2越大（接近于1），所拟合的回归方程越优。

 

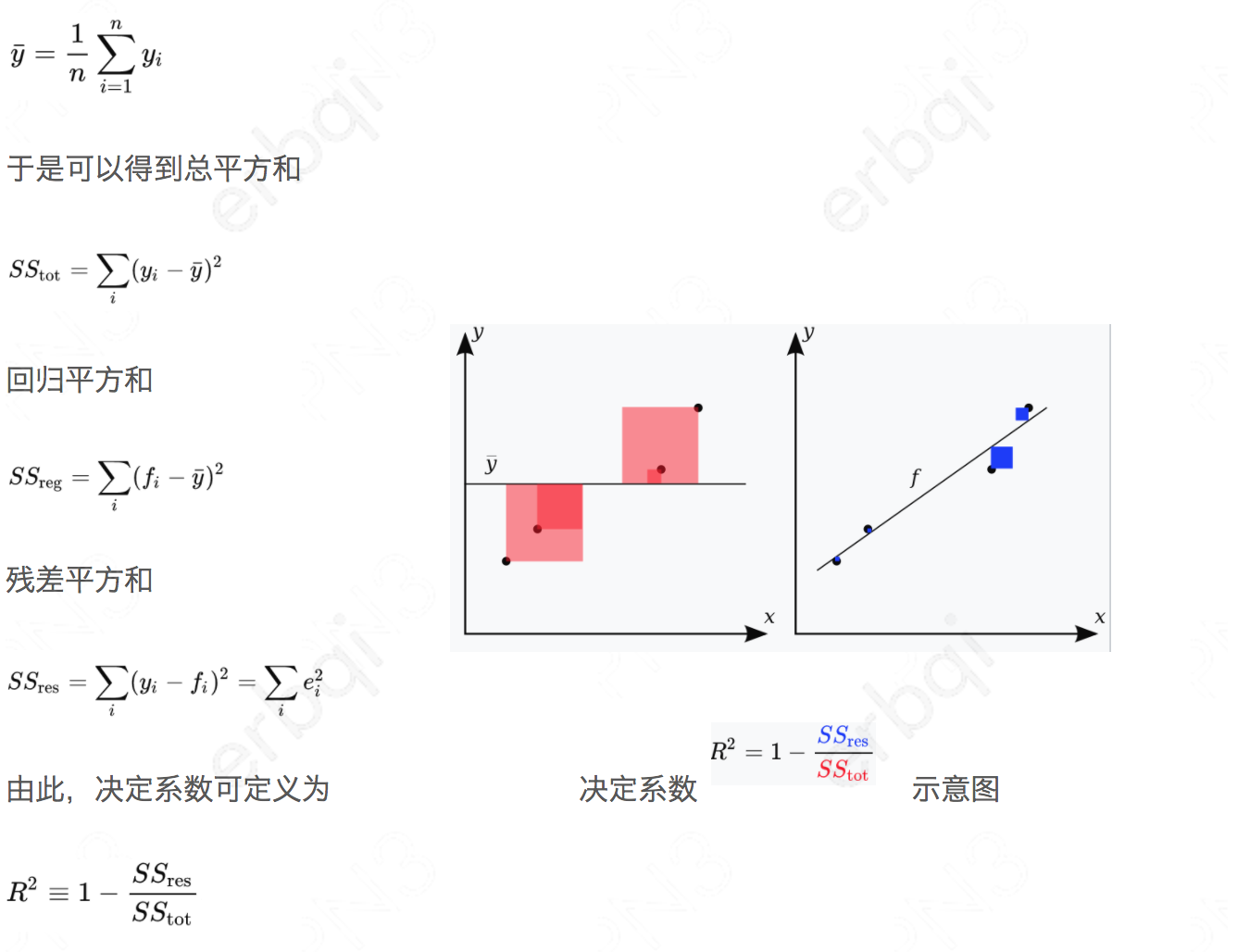
假设一数据集包括y1,...,yn共n个观察值，相对应的模型预测值分别为f1,...,fn。定义残差ei = yi − fi，平均观察值为

虽然R2可以用来评价回归方程的优劣，但随着自变量个数的增加，R2将不断增大（因为自变量个数的增加，意味着模型的复杂度升高，对样本数据的拟合程度会提高）。

若对两个具有不同个数自变量的回归方程进行比较时，不能简单地用R2作为评价回归方程的标准，还必须考虑方程所包含的自变量个数的影响，此时可用校正的决定系数（R2-adjusted）

其中n是样本数量，p是模型中变量的个数，当变量个数为0时，修正和原始的R方是一样的

就是相当于给变量的个数加惩罚项。换句话说，如果两个模型，样本数一样，R2一样，那么从修正R2的角度看，使用变量个数少的那个模型更优。

至于R2大于多少才有意义呢？这时我们可以看另外一个指标：复相关系数（Multiple correlation coefficient）R，R是决定系数R2的平方根，可用来度量因变量Y与多个自变量间的线性相关程度，即观察值Y与估计值之间的相关程度。

相关系数要在0.7~0.5才有意义，因此，R2应大于0.5*0.5=0.25，所以有种观点认为，在直线回归中应R2大于0.3才有意义。

还是来看下一个简单的例子，看下简单的平滑预测的R平方有多少

import numpy as np 

def r_square(y,f):
    y,f = np.array(y),np.array(f)
    y_mean = y.mean()
    SStot  = sum(np.power((y-y_mean),2))
    SSres  = sum(np.power(y-f,2))
    return 1.0 - 1.0*SSres/SStot

def smooth_(squences,period=5):
    res = []
    gap = period/2
    right = len(squences)
    for i in range(right):
        res.append(np.mean(squences[i-gap if i-gap > 0 else 0:i+gap if i+gap < right else right]))
    return res 

httpspeedavg = np.array([1821000, 2264000, 2209000, 2203000, 2306000, 2005000, 2428000,
       2246000, 1642000,  721000, 1125000, 1335000, 1367000, 1760000,
       1807000, 1761000, 1767000, 1723000, 1883000, 1645000, 1548000,
       1608000, 1372000, 1532000, 1485000, 1527000, 1618000, 1640000,
       1199000, 1627000, 1620000, 1770000, 1741000, 1744000, 1986000,
       1931000, 2410000, 2293000, 2199000, 1982000, 2036000, 2462000,
       2246000, 2071000, 2220000, 2062000, 1741000, 1624000, 1872000,
       1621000, 1426000, 1723000, 1735000, 1443000, 1735000, 2053000,
       1811000, 1958000, 1828000, 1763000, 2185000, 2267000, 2134000,
       2253000, 1719000, 1669000, 1973000, 1615000, 1839000, 1957000,
       1809000, 1799000, 1706000, 1549000, 1546000, 1692000, 2335000,
       2611000, 1855000, 2092000, 2029000, 1695000, 1379000, 2400000,
       2522000, 2140000, 2614000, 2399000, 2376000])
httpavg = np.round((1.0*httpspeedavg/1024/1024).tolist(),2)
smooth = np.round(smooth_((1.0*httpspeedavg/1024/1024).tolist(),5),2)

print r_square(httpavg,smooth)
# 0.711750424322

也就是71%的网络变化情况可以用平滑预测来解释