noip模拟测试18

打开比赛第一眼——超级树？

点开——原题

百感交集……

欣喜于发现是半年前做过两遍的原题

紧张于如果A不了比较尴尬

绝望于发现根本不会做了

瞟了一眼t1，瞅了一眼t2，嗯……开始搞t3

10分钟打完暴力，开始dp退柿子。然而一个半小时过去了，发现经过一番挫折才终于想起来那个阴间的状态

上了个厕所，看了下表不早了，得开始写前面的了，好恋恋不舍~

再看t2，10分钟打了个很不确定的二分

再看t1，20分钟推了个没有证明的结论

写完都交了

看了下表大概九点半多了，感觉两个小时一事无成，但还是铁下心又回去推t3。

写了好几草稿纸的柿子，手模 \(n=3\) 的情况，老是差那么一点点……

听见隔壁大佬自言自语说t1好难处理，估计是挂了

上厕所看见好多人都在看t2，估计二分是伪了

心里想着算了吧，t3没A就没A吧，估计好多人也忘了

但一想要是现在停下来两个多小时努力就白费了

又一想这题上次也是我讲的肯定是会做哒

再一想只要A掉这道题排名肯定也不会差

于是一直推一直推直到结束也没弄出来……

于是得到了史无前例的糟糕成绩……

题解

---

好了好了，先回归正题~

A. 星级旅行

首先，要看出这道题的本质是求欧拉路。相当于将每条边复制一下，这时每个点的度数都成为偶数，然后去掉两条边使得整个图有欧拉路

由于这道题里光明正大地说有自环，记自环数量为 \(tot\)，于是可以分为三种情况：

1. 删除两个自环，这时这两个点的度数都减少2（或者一个点减少4），满足题意，答案为 \(C_{tot}^2\)
2. 删除一个自环和一条边，这时边两端的点度数减少1，成为奇数度点，分别成为起点和终点，答案为 \(tot*(m-tot)\)
3. 删除两条边，这时有特殊要求是这两条边有一个公共的端点，产生两个奇数度点，此时答案为 \(\sum C_{deg_i}^2\)

查看代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
const int maxm=4e5+5;
int n,m,deg[maxn],cnt,hd[maxn],tot,num[maxn],num1,x,y;
long long ans;
bool vis[maxm];
int read(){
	int x=0,f=1;
	char ch=getchar();
	while(!isdigit(ch)){
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(isdigit(ch)){
		x=x*10+ch-48;
		ch=getchar();
	}
	return x*f;
}
struct Edge{
	int nxt,to;
}edge[maxm];
void add(int u,int v){
	edge[++cnt].nxt=hd[u];
	edge[cnt].to=v;
	hd[u]=cnt;
	return ;
}
void dfs(int u,int from){
	vis[u]=true;
	num[from]++;
	for(int i=hd[u];i;i=edge[i].nxt){
		int v=edge[i].to;
		if(!vis[v])dfs(v,from);
	}
	return ;
}
int main(){
	n=read();
	m=read();
//	cnt=1;
	int root=0;
	for(int i=1;i<=m;i++){
		x=read();
		y=read();
		if(x==y){
			tot++;
		}
		else{
			add(x,y);
			add(y,x);
			root=i;
			deg[x]++;
			deg[y]++;
		}
	}
	for(int i=1;i<=n;i++){
		dfs(i,i);
	}
	for(int i=1;i<=n;i++){
		if(num[i]>1)num1++;
	}
	if(num1>1||tot==m){
		cout<<0;
		return 0;
	}
	ans=1ll*tot*(m-tot);
	ans+=1ll*tot*(tot-1)/2;
	for(int i=1;i<=n;i++){
		if(deg[i]>=2)ans+=1ll*deg[i]*(deg[i]-1)/2;
	}
	cout<<ans;
	return 0;
}

B. 砍树

首先说一下错误的做法——二分

这题其实没有单调性（取模运算似乎往往都没有）

比如可以举出栗子

5 10 25

当模数取5的时候答案灰常小，而模数取4和6的时候又会很大

其实嘛……这是一个老老实实推柿子的题

这道题需要满足的条件是

\(\sum_{i=1}^{n} d-(a_i \%d)\le k\)，其中1求和部分当 \(a_i\) 模d等于0时以0计算

\(d-\sum_{i=1}^{n} a_i-\left \lfloor \frac{a_i}{d} \right \rfloor * d \le k\)

\(d*n-sum+\sum_{i=1}^{n} \left \lfloor \frac{a_i}{d} \right \rfloor * d \le k\)

\(\sum_{i=1}^{n} \left \lfloor \frac{a_i}{d} \right \rfloor \le \left \lfloor \frac{k+sum}{d} \right \rfloor -n\)

现在再观察柿子，发现右边 \(k+sum\) 和 \(n\) 都是定值，而除 \(d\) 取整特别难受

于是可以想到一个高级科技——整除分块儿~

右边分块后会有根号种取值，每种取值对应 \(d\) 的一段连续区间 \(\left [l,r \right ]\)，暴力计算左边验证是否满足条件

观察左式，当 \(d\) 越大时值越小，也越容易满足条件，于是每次只需要贪心地选取区间的 \(r\) 进行验证并更新答案即可

查看代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=105;
#define int long long
int n,k,a[maxn],sum,tot,ans,l,r,x;
int read(){
	int x=0,f=1;
	char ch=getchar();
	while(!isdigit(ch)){
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(isdigit(ch)){
		x=x*10+ch-48;
		ch=getchar();
	}
	return x*f;
}
bool check(int limit){
	int sum1=0;
	for(int i=1;i<=n;i++){
		int x=a[i]%limit;
		if(!x)x=limit;
		sum1+=limit-x;
	}
	if(sum1<=k)return true;
	return false;
}
signed main(){
	n=read();
	k=read();
	for(int i=1;i<=n;i++){
		a[i]=read();
		sum+=a[i];
	}
	tot=sum+k;
//	cout<<check(3);
//	cout<<tot<<endl;
	while(r<tot){
		l=r+1;
		x=tot/l;
		r=min(tot/x,tot);
//		cout<<l<<" "<<r<<" "<<check(r)<<endl;
		if(check(r))ans=max(ans,r);
	}
	cout<<ans;
	return 0;
}

C. 超级树

咳咳——这道恶心的题

这回细细地写一下这道题

首先说一下为什么状态不能设计成一维的

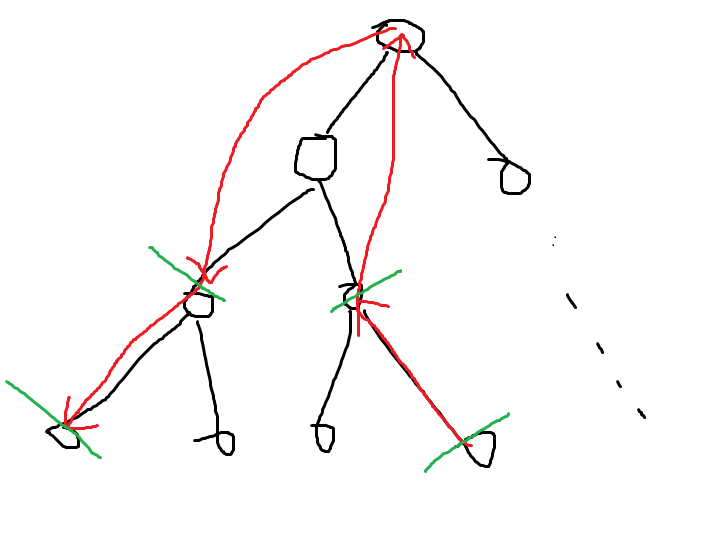
像上图一样，在处理当前节点是会有很儿子节点中的两条路径与根节点拼接形成新的路径，而一维状态只能处理当前层节点的信息，于是显然不适用

于是改进，状态为：\(f_{i,j}\) 表示 \(i\) 级超级树中存在 \(j\) 条互不相交的路径的方案数

则答案是 \(f_{k,1}\)

再来看转移，首先观察超级树，长得有一个特点——就是根节点将树劈成了两半，而横跨根节点的路径最多一条。

于是对于 \(i\) 级超级树左子树有 \(j\) 条路径，右子树有 \(k\) 条路径，向 \(i+1\) 级超级树转移时，可以分为四种情况：

• 不选取根节点，也不拼合路径，此时大的超级树有 \(j+k\) 条路径：\(f_{i+1,j+k}+=f_{i,j}*f_{i,k}\)
• 选取根节点，不拼合路径，此时根节点自成一条路径，大的超级树有 \(j+k+1\) 条路径：\(f_{i+1,j+k+1}+=f_{i,j}*f_{i,k}\)
• 选取根节点，根节点与左或右子树中的一条路径拼合，大的超级树有 \(j+k\) 条路径，由于可以接在头也可以接在尾，需要乘2：\(f_{i+1,j+k}+=2*(j+k)*f_{i,j}*f_{i,k}\)
• 选取根节点，根节点将两条路径串联，大的超级树有 \(j+k-1\) 条路径，由于可以头接尾也可以尾接头，需要乘2：\(f_{i+1,j+k-1} += 2*C_{j+k}^{2}*f_{i,j}* f_ {i,k}\)

回头算一下时间复杂度，发现是 \(n^3\) 的，考虑优化

观察一下转移的柿子和最后的目标，由于每次升级条数最多减少1，而最终条数为1，所以满足 \(i+j+k \le n\) 即可，大大减少复杂度

查看代码

#include<bits/stdc++.h>
using namespace std;
int n;
long long f[305][305],mod;
int main(){
	cin>>n>>mod;
	f[1][1]=f[1][0]=1;
	for(int i=1;i<=n-1;i++){
		for(int j=0;j<=n-i+1;j++){
			for(int k=0;k<=n-j-i+2;k++){
				f[i+1][j+k]=(f[i+1][j+k]+f[i][j]*f[i][k]%mod)%mod;
				f[i+1][j+k+1]=(f[i+1][j+k+1]+f[i][j]*f[i][k]%mod)%mod;
				f[i+1][j+k]=(f[i+1][j+k]+2ll*f[i][j]%mod*f[i][k]%mod*(j+k)%mod)%mod;
				f[i+1][j+k-1]=(f[i+1][j+k-1]+(j+k)*(j+k-1)%mod*f[i][k]%mod*f[i][j]%mod)%mod;
			}
		}
	}
	cout<<f[n][1]%mod;
	return 0;
}

Summary

平时不考不知道，一考发现竟然做过两遍的题再出来还是不会做，每场考试的改题过程存在很大的漏洞，因此：

• 看懂思路后独立完成代码
• 减少改题提交次数
• A掉题以后花时间沉淀反思
• 搜集尝试不同的思路
• 每次考试后跟进博客

而且，万一再有原题——不要惊慌，不要紧张，照常按难度做题即可——不要吊死在一棵树上~