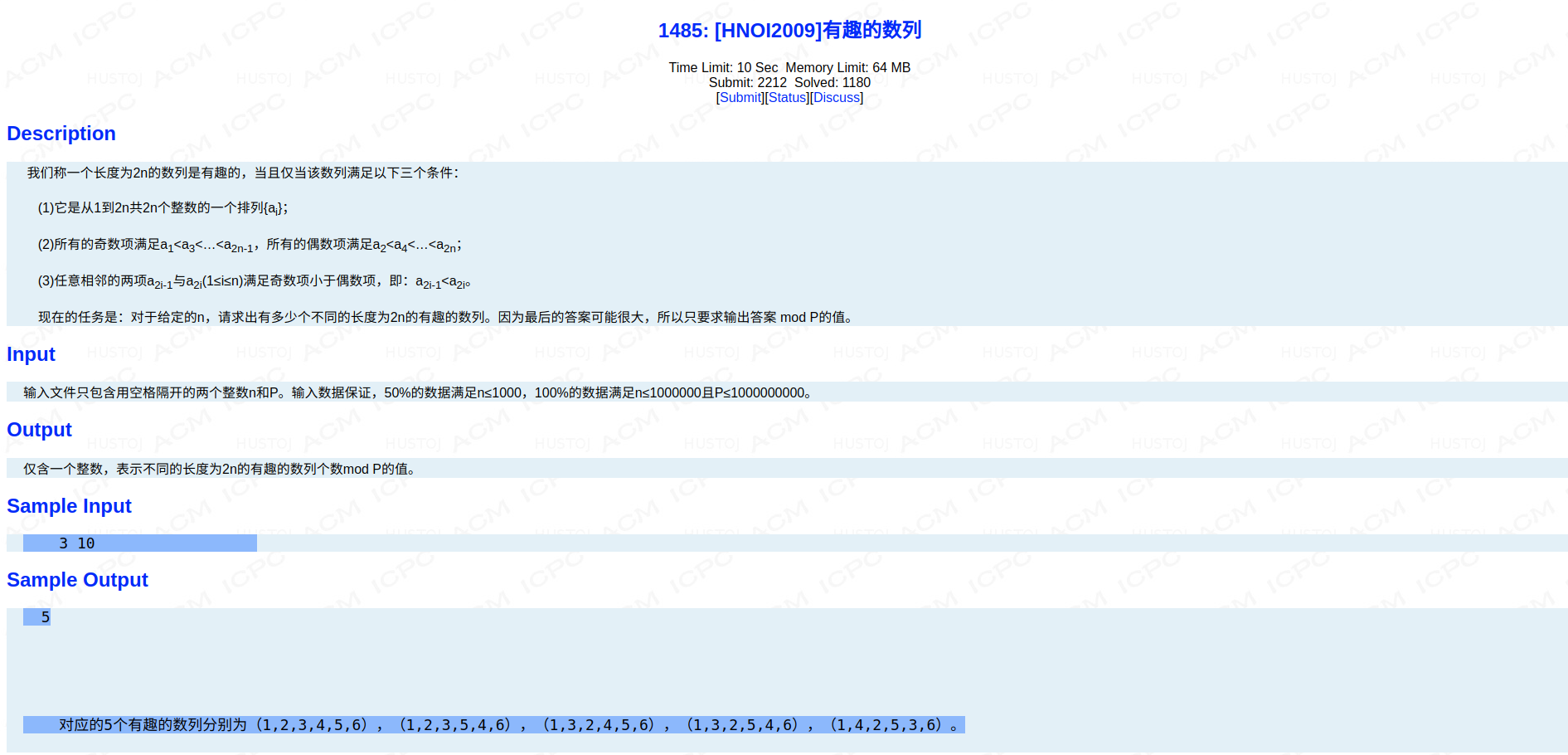
BZOJ1485: [HNOI2009]有趣的数列(卡特兰数＋快速幂)

题目链接

传送门

题面

思路

打表可以发现前六项分别为１,2,5,12,42,132，加上\(ｎ=0\)时的１构成了卡特兰数的前几项。

看别人的题解说把每一个数扫一遍，奇数项当成入栈，偶数项当成出栈，然后就是卡特兰数的公式了。

卡特兰数公式为:

\[\begin{aligned}
&C_{2n}^{n}-C_{2n}^{n+1}&\\
=&\frac{2n!}{n!n!}-\frac{2n!}{(n+1)!(n-1)!}&
\end{aligned}
\]

因为要对Ｐ取模，但是Ｐ不一定是素数，因此使用快速幂等方法求逆元是无法实现的，因此这个时候我们就将分子的素数的指数求出来然后减去分明的素数的指数，最后通过快速幂来进行求解即可。

代码实现如下

#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> piL;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;

#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) x&(-x)
#define name2str(name) (#name)
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define FIN freopen("in","r",stdin)
#define IO ios::sync_with_stdio(false),cin.tie(0)

const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 2e6 + 7;
const double pi = acos(-1);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3fLL;

int n, m, P;
int p[maxn], isp[maxn], cnt[maxn];

void init() {
    for(int i = 2; i <= 2 * n; ++i) p[i] = 1;
    for(int i = 2; i * i <= 2 * n; ++i) {
        if(p[i]) {
            for(int j = i * i; j <= 2 * n; j += i) {
                p[j] = 0;
            }
        }
    }
    for(int i = 2; i <= 2 * n; ++i) {
        if(p[i]) {
            isp[m++] = i;
        }
    }
}

LL qpow(LL x, int n) {
    LL res = 1;
    while(n) {
        if(n & 1) res = res * x % P;
        x = x * x % P;
        n >>= 1;
    }
    return res;
}

void get_num(int x, int sign) {
    for(int i = 0; i < m && isp[i] <= x; ++i) {
        LL num = isp[i];
        while(num <= x) {
            cnt[i] += sign * x / num;
            num *= isp[i];
        }
    }
}

int solve(int n, int k) {
    for(int i = 0; i < m; ++i) cnt[i] = 0;
    get_num(n, 1);
    get_num(k, -1);
    get_num(n - k, -1);
    int res = 1;
    for(int i = 0; i < m; ++i) {
        res = (1LL *  res * qpow(isp[i], cnt[i])) % P;
    }
    return res;
}

int main() {
#ifndef ONLINE_JUDGE
    FIN;
#endif
    scanf("%d%d", &n, &P);
    init();
    printf("%d\n", (solve(2 * n, n) - solve(2 * n, n + 1) + P) % P);
    return 0;
}