[hdu 1568] Fibonacci数列前4位

2007年到来了。经过2006年一年的修炼，数学神童zouyu终于把0到100000000的Fibonacci数列
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部给背了下来。
接下来，CodeStar决定要考考他，于是每问他一个数字，他就要把答案说出来，不过有的数字太长了。所以规定超过4位的只要说出前4位就可以了，可是CodeStar自己又记不住。于是他决定编写一个程序来测验zouyu说的是否正确。

 

Input

输入若干数字n(0 <= n <= 100000000)，每个数字一行。读到文件尾。

 

Output

输出f[n]的前4个数字（若不足4个数字，就全部输出）。

 

Sample Input

0
1
2
3
4
5
35
36
37
38
39
40

 

Sample Output

0 1 1 2 3 5 9227 1493 2415 3908 6324 1023

 

思路：

求Fibonacci数列的前4位数，如果直接递推或用矩阵递推会存不下，这里用公式来直接求。

 

求12345678的前4位，可以先取对数log10(12345678) = log10(1.2345678*10^7) = log10(1.2345678)+7

log10(1.2345678) < 1, 所以对原数向下取整可得到t = log10(1.2345678), 再取pow(10.0, t),可得到1.2345678

运用double只精确保留指定位数的小数的特性来舍去后面的数，保留前面的数。

 

这题中：Fibonacci有如下公式：

经过化简后可得：

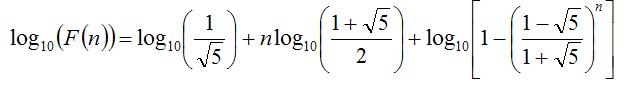
也就是先取以10为底的对数，再取指数，得到整数及前几位小数部分

#include <iostream>
#include <stdio.h>
#include <cstring>
#include <math.h>
#include <algorithm>
 
using namespace std;
int a[];  //<=25
 
int main()
{
    //freopen("1.txt", "r", stdin);
    a[] = ; a[] = ;
    for (int i = ; i <= ; i++) {
        a[i] = a[i-]+a[i-];
    }
    int N;
    while (~scanf("%d", &N)) {
        if (N <= ) {
            printf("%d\n", a[N]);
            continue;
        }
        double t = ;
        double s = (sqrt(5.0)+1.0)/2.0;
        t = -0.5*log(5.0)/log(10.0) + (double)N*log(s)/log(10.0);
        t = t-floor(t);
        t = pow(10.0, t);
        while (t < )
            t *= ;
        printf("%d\n", (int)t);
    }
 
    return ;
}