HS 光流法详解
前言
本文较为详细地介绍了一种经典的光流法 - HS 光流法。
光流法简介
当人的眼睛与被观察物体发生相对运动时,物体的影像在视网膜平面上形成一系列连续变化的图像,这一系列变化的图像信息不断 "流过" 视网膜,好像是一种光的 "流",所以被称为光流。
光流是基于像素点定义的,所有光流的集合称为光流场。通过对光流场进行分析,可以得到物体相对观察者的运动场。在这过程中分析的算法称为光流法。
HS 光流法的推导
HS光流计算基于物体移动的光学特性的两个假设:
1. 运动物体的灰度在很短的间隔时间内保持不变
2. 给定邻域内的速度向量场变化是缓慢的
由 1 可得:
 (1)
(1)
上式右边在 x y 处泰勒展开,得:
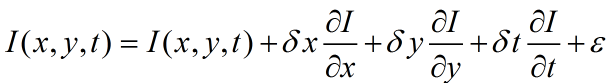 (2)
(2)
ε 是包含有 δx,δy 和 δt 的二阶和更高阶项。两边减去 I(x,y,t),再除以δt有:
 (3)
(3)
O (δt) 是含δt的一个小量。在极限中当δt->0时,上式变成:
 (4)
(4)
令 u = dx/dt v = dy / dt,得:
 (5)
(5)
这条式子就是光流约束方程,它反映了灰度与速度的一个对应关系。
但,一个式子中有两个变量:u 和 v,显然不能将速度解出,因此需要引入一个新的条件:光流的全局平滑约束条件。
即 u 和 v 随着像素点移动而发生的改变是缓慢的,局部区域的变化不大,尤其是在目标做无变形刚体运动时,局部区域速度的空间变化率为0。
因此,引入以下速度平滑项:
 (6)
(6)
对于所有的像素点,需要满足上式和最小。
综合光流约束条件 (5) 和速度平滑约束条件 (6),可建立以下的极小化方程:
 (7)
(7)
式中的 α 是平滑权重系数,表示速度光滑项所占的权重。
即:
 (8)
(8)
采用变分计算,根据欧拉方程,
 (9)
(9)
 (10)
(10)
得到:
 (11)
(11)
 (12)
(12)
式中,拉普拉斯算子可以用某一点的速度与其周围速度平均值之差来近似,有:
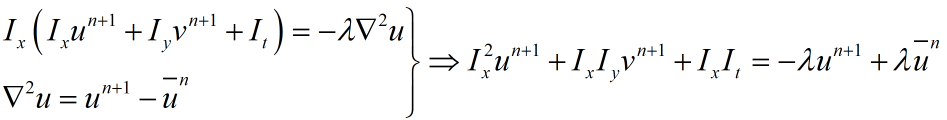 (13)
(13)
 (14)
(14)
化简 (13) 和 (14),可得: ( 这一步运算量比较大 )
 (15)
(15)
 (16)
(16)
这样便可以考虑使用迭代法进行求解了,但在此之前,还需要明确其中几个量的求法。
对于 u 和 v 的均值,采用九点差分格式进行计算:
 (17)
(17)
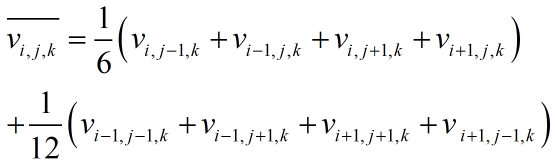 (18)
(18)
而对于其中的灰度梯度,可以采用以下方法近似计算:
 (19)
(19)
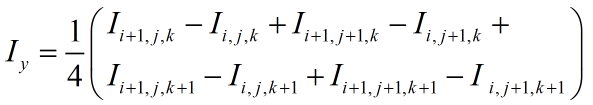 (20)
(20)
 (21)
(21)
至此,所有的量都已明确下来,输入前后两帧灰度进行迭代运算便可以得到速度场了,下面是具体的执行过程。
HS光流法执行流程图

1. 读取雷达拼图数据并初始化
2. 计算求解点的灰度梯度
3. 设定速度平滑权重系数( 一般设为1 ),初始速度( 一般设为0 ),迭代误差等。
4. 计算 k-1 次速度平均值
5. 计算 k 次迭代的速度值
6. 计算两次迭代光流值的误差,如果小于给定误差阈值,或者者迭代次数超过迭代次数,则计算过程结束,否则进行k+1次迭代。
HS 光流法详解的更多相关文章
- HS光流算法详解<转载>
HS 光流法详解 前言 本文较为详细地介绍了一种经典的光流法 - HS 光流法. 光流法简介 当人的眼睛与被观察物体发生相对运动时,物体的影像在视网膜平面上形成一系列连续变化的图像,这一系列变化的图像 ...
- 光流法详解之一(LK光流)
Lucas–Kanade光流算法是一种两帧差分的光流估计算法.它由Bruce D. Lucas 和 Takeo Kanade提出 [1]. LK光流法有三个假设条件: 1. 亮度恒定:一个像素点随着时 ...
- 光流法详解之二(HS光流)
Horn–Schunck光流算法[1]是一种全局方法估算光流场. 参考博文:https://blog.csdn.net/hhyh612/article/details/79216021 假设条件: H ...
- RAII惯用法详解
[1]什么是RAII惯用法? RAII是Resource Acquisition Is Initialization的缩写,意为“资源获取即初始化”. 它是C++之父Bjarne Stroustrup ...
- SLAM入门之视觉里程计(6):相机标定 张正友经典标定法详解
想要从二维图像中获取到场景的三维信息,相机的内参数是必须的,在SLAM中,相机通常是提前标定好的.张正友于1998年在论文:"A Flexible New Technique fro Cam ...
- KKT条件和拉格朗日乘子法详解
\(\frac{以梦为马}{晨凫追风}\) 最优化问题的最优性条件,最优化问题的解的必要条件和充分条件 无约束问题的解的必要条件 \(f(x)\)在\(x\)处的梯度向量是0 有约束问题的最优性条件 ...
- 扩展欧几里得算法详解(exgcd)
一.前言 本博客适合已经学会欧几里得算法的人食用~~~ 二.扩展欧几里得算法 为了更好的理解扩展欧几里得算法,首先你要知道一个叫做贝祖定理的玄学定理: 即如果a.b是整数,那么一定存在整数x.y使得$ ...
- lca(最近公共祖先(在线)) 倍增法详解
转自大佬博客 : https://blog.csdn.net/lw277232240/article/details/72870644 描述:倍增法用于很多算法当中,通过字面意思来理解 LCA是啥呢 ...
- 后缀数组 DC3构造法 —— 详解
学习了后缀数组,顺便把DC3算法也看了一下,传说中可以O(n)复杂度求出文本串的height,先比较一下倍增算法和DC3算法好辣. DC3 倍增法 时间复杂度 O(n)(但是常数很大) O(nlo ...
随机推荐
- Adobe Photoshop CS6下载安装
下载链接 http://yunpan.cn/cACgP6Lv5ygit (提取码:f37a) 第一步关键是断开网络,拔掉网线或断开无线 点击登录后,如果没有进入下面的界面,检查是否断网成功 至于选择安 ...
- input或其他元素的左上角和左下角单独圆角实现
border-bottom-left-radius:6px;/*左下角圆角*/ border-top-left-radius: 6px;/*左上角圆角*/
- java基础 静态 static 问在多态中,子类静态方法覆盖父类静态方法时,父类引用调用的是哪个方法?
多态 package com.swift.jiekou; public class Jicheng_Tuotai_jingtai_diaoyong { public static void main( ...
- 【iOS】史上最全的iOS持续集成教程 (上)
:first-child{margin-top:0!important}.markdown-body>:last-child{margin-bottom:0!important}.markdow ...
- C++ 编写的解码器小程序 map
c++ prime 5 ex11_4 代码如下 // ex11_4_word_transform.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h&quo ...
- 关于Ubuntu 16.04 pip安装Docker-Compose
$ sudo apt-get update 安装pip: $ sudo apt-get install python-pip 卸载旧版本docker-compose: $ sudo pip unins ...
- Spring Cloud 入门 Consul-Server服务注册
前面见过 Eureka服务注册,需要单独启用一个springboot项目 :这里介绍一个 spring cloud consul 服务, 只需要安装相关客户端,启动它就行: 1.安装Consul(以 ...
- linux 基本命令笔记
nohup [process] & 后台挂起命令nohup 挂起& 后台运行 python3 manage.py runserver 0.0.0.0:8080 python -r 递 ...
- Guava Cache 工具类 [ GuavaCacheUtil ]
pom.xml <dependency> <groupId>com.google.guava</groupId> <artifactId>guava&l ...
- scrapy--selenium(二)
今天学习了很多,还是想给大家讲一讲正题:scrapy的动态加载AJax的网页爬取:selenium.让我们开始 三: 针对大型电商网站:京东网,因为比较有代表性,爬出来有点小成就.先给大家看下效果图. ...
