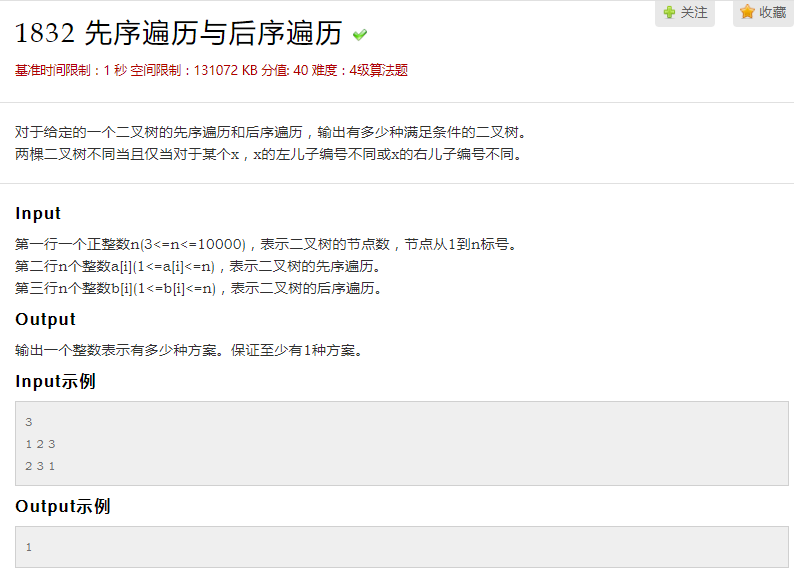
51nod 1832 前序后序遍历

思路：设只有一颗子树的节点有ans个设前序边历数组为pre[100],后序遍历数组为pos[100]；前序遍历的第二个元素是A的一个子节点左右节点不知，设ax-ay表示一个树的前序遍历，bx-by表示后序遍历，可知如果pre[ax+1] = pos[i] 且 i = by-1,上一个根节点只有一个子树，此时令计数变量ans++；如果i ！= b2-1，很明显存在左右子树，此时应分别处理此时左子树为的前后序边历分别为：ax+1~ax+1+i-bx,bx~i,右子树为：ax+1+i-bx~ay,i+1~by-1；最后计算2^ans即为数的数目。值得注意的是：由于ans比较大，2^ans太大，需要用到大数乘法

 #include<iostream>
 #include<algorithm>
 #include<cstring>

 using namespace std;
 typedef long long LL;
 const int maxn = ;
 int n, pre[maxn], pos[maxn], ans, index[maxn];
 int a[maxn * ];
 void dfs(int ax, int ay, int bx, int by)
 {
     if (ax >= ay)return;
     int i = index[pre[ax + ]];
     if (i == by - )ans++;
     dfs(ax + , ax +  + i - bx, bx, i);
     dfs(ax +  + i - bx + , ay, i + , by - );
 }
 int main()
 {
     ios::sync_with_stdio(false);
     while (cin >> n) {
         ans = ;
         for (int i = ; i <= n; i++)cin >> pre[i];
         for (int i = ; i <= n; i++) {
             cin >> pos[i]; index[pos[i]] = i;
         }
         dfs(, n, , n);
         memset(a, , sizeof(a));
         a[] = ; n = ;
         for (int i = ; i <= ans; i++) {
             for (int j = ; j <= n; j++)
                 a[j] *= ;
             for (int j = ; j <= n; j++)
                 if (a[j] >= ) {
                     a[j + ] = a[j + ] + a[j] / ;
                     a[j] %= ;
                     n = max(n, j + );
                 }
         }
         for (int i = n; i >= ; i--)
             cout << a[i]; cout << endl;
     }
     return ;
 }