（POJ - 1050）To the Max 最大连续子矩阵和

Given a two-dimensional array of positive and negative integers, a sub-rectangle is any contiguous sub-array of size 1*1 or greater located within the whole array. The sum of a rectangle is the sum of all the elements in that rectangle.
In this problem the sub-rectangle with the largest sum is referred to as the maximal sub-rectangle. 

As an example, the maximal sub-rectangle of the array: 

0 -2 -7 0 

9 2 -6 2 

-4 1 -4 1 

-1 8 0 -2 

is in the lower left corner: 

9 2 

-4 1 

-1 8

and has a sum of 15.

Input

The input consists of an N * N array of integers. The input begins with a single positive integer N on a line by itself, indicating the size of the square two-dimensional array. This is followed by N^2 integers separated by whitespace (spaces and newlines).
These are the N^2 integers of the array, presented in row-major order. That is, all numbers in the first row, left to right, then all numbers in the second row, left to right, etc. N may be as large as 100. The numbers in the array will be in the range [-127,127].

Output

Output the sum of the maximal sub-rectangle.

Sample Input

4

0 -2 -7 0

9 2 -6 2

-4 1 -4 1

-1 8 0 -2

Sample Output

15

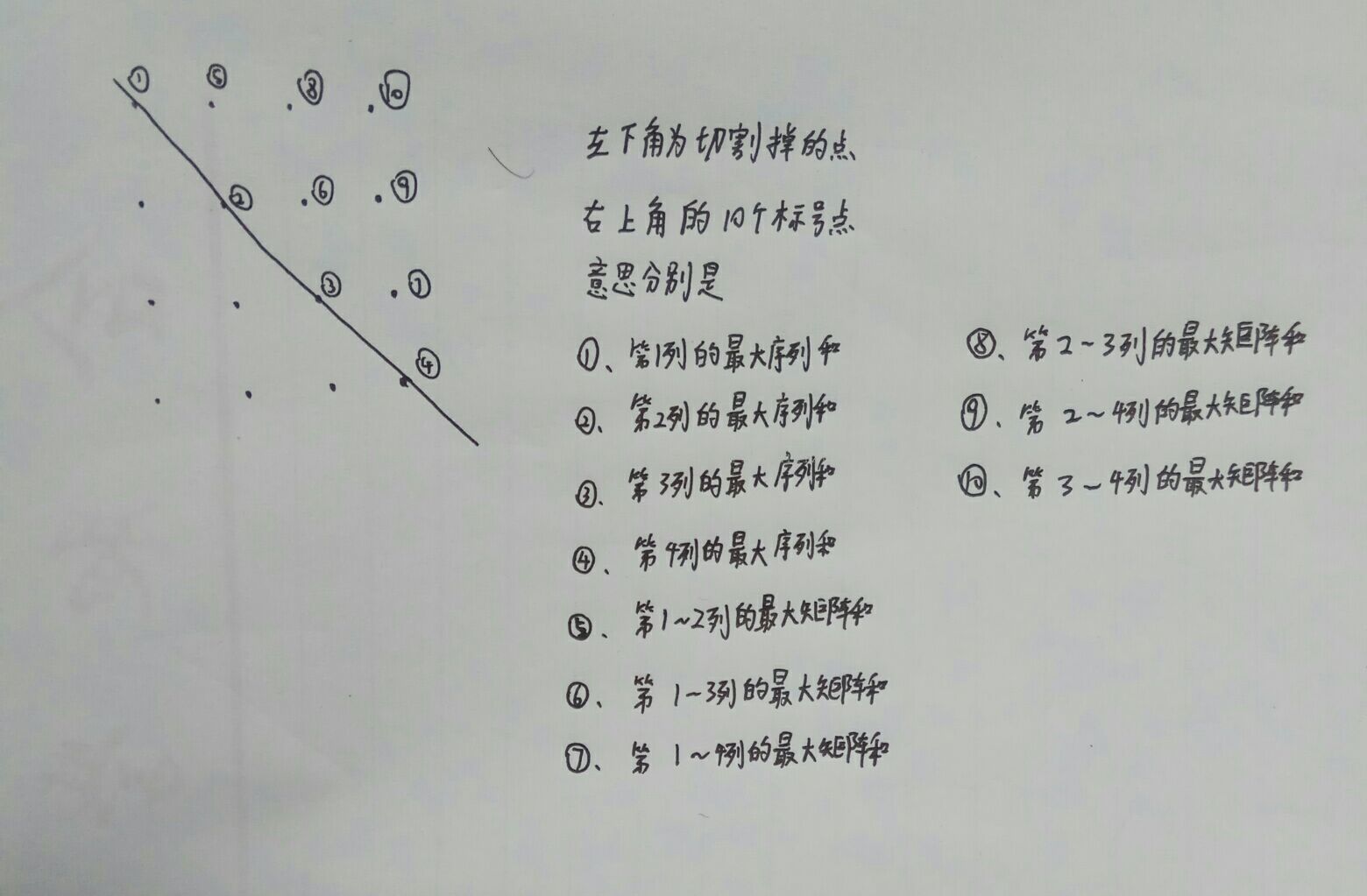
解题报告：这道题真的是感人，状态转移方程干到我怀疑人生，最后终于搞明白了，下面附上理解图，希望能便于大家理解此题的DP方程

#include <bits/stdc++.h>
using namespace std;

int map[110][110],dp[110][110];

int main()
{
    //freopen("input.txt","r",stdin);
	int N,a;
    while(~scanf("%d",&N) && N)
    {
        memset(map,0,sizeof(map));
        memset(dp,0,sizeof(dp));

		for(int i = 1; i <= N; i++)
            for(int j = 1; j <= N; j++)
            {
                scanf("%d",&a);
                map[i][j] = map[i][j-1] + a;
                //map[i][j]表示第i行前j列的和
            }

        int Max = -0xffffff0;

		for(int j = 1; j <= N; j++)
            for(int i = 1; i <= j; i++)
            {
                dp[i][j] = 0;

                for(int k = 1; k <= N; k++)
                {
                    dp[i][j]= max(dp[i][j]+map[k][j]-map[k][i-1],map[k][j]-map[k][i-1]);
                    if(dp[i][j] > Max)

                        Max = dp[i][j];
                }
            }

        printf("%d\n",Max);
    }
    return 0;
}