[转] LCA与Tarjan

转载：http://m.blog.csdn.net/blog/u013076044/41875009#

在线算法与离线算法的定义

在计算机科学中，一个在线算法是指它可以以序列化的方式一个个的处理输入，也就是说在开始时并不需要已经知道所有的输入。相对的，对于一个离线算法，在开始时就需要知道问题的所有输入数据，而且在解决一个问题后就要立即输出结果。例如，选择排序在排序前就需要知道所有待排序元素，然而插入排序就不必。

因为在线算法并不知道整个的输入，所以它被迫做出的选择最后可能会被证明不是最优的，对在线算法的研究主要集中在当前环境下怎么做出选择。对相同问题的在线算法和离线算法的对比分析形成了以上观点。如果想从其他角度了解在线算法可以看一下 流算法（关注精确呈现过去的输入所使用的内存的量），动态算法（关注维护一个在线输入的结果所需要的时间复杂度）和在线机器学习。

那么LCA的离线tarjan算法是什么呢，众所周知，taejan算法基本就是一个dfs，那么这个也是用一个dfs来完成的，那思想是什么呢？

首先先用把要求的值存下来，就是所谓的离线一下， 然后dfs什么呢，就是先判断有没有再query里的，如果在query里并且那个已经被处理过了，并且他们的公共祖先没有被标记掉，那么就可以求这两个点之间的距离了。
接下来就是各种把他的未标记节点dfs一遍
然后就求出答案了
步骤：
tarjan算法的步骤是(当dfs到节点u时):
1 在并查集中建立仅有u的集合,设置该集合的祖先为u
1 对u的每个孩子v:
   1.1 tarjan之
   1.2 合并v到父节点u的集合,确保集合的祖先是u
2 设置u为已遍历
3 处理关于u的查询,若查询(u,v)中的v已遍历过,则LCA(u,v)=v所在的集合的祖先
贴图解释一下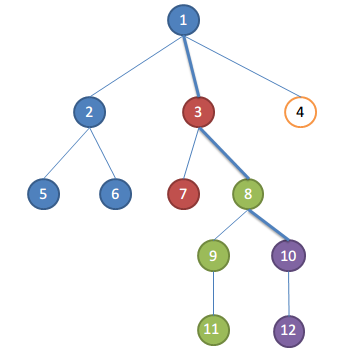

如图：前面处理的时候能把每一个每一个颜色的处理为一个集合，并且用并查集随着先后顺序也会发现lca再不断的变化，并且不会错，这是为什么呢，这就是奇妙的dfs
因为他的查询和处理是同步的，所以他是不会错的
比如查询5 6
那么可以知道，现在5,6的祖先是2，并且findset（6）为2，
查询   2 8
那么2 ，8的lca就是1
因为是先处理的2，所以再8的地方2已经被处理过了，所以现在findset（2）=1；
代码如下：

void dfs(int u){
     for(int i=;i<query[u].size();i++){
       int v=query[u][i].to;
       if(vis[v]&&ans[query[u][i].w]==-&&!mark[findset(v)]){
        ans[query[u][i].w]=dis[u]+dis[v]-*dis[findset(v)];
       }
     }
     for(int i=;i<mp[u].size();i++){
         int v=mp[u][i].to;
         if(!vis[v]){
             vis[v]=;
             dis[v]=dis[u]+mp[u][i].w;
             dfs(v);
             par[v]=u;
         }
     }
}